题目内容

2．已知x＞0，y＞0，且x+16y=xy，则x+y的最小值为25．

分析 由x+16y=xy可得$\frac{16}{x}$+$\frac{1}{y}$=1．根据基本不等式即可得到答案

解答 解：已知x＞0，y＞0，且x+16y=xy．
即：$\frac{16}{x}$+$\frac{1}{y}$=1．
利用基本不等式：则x+y=（x+y）（$\frac{16}{x}$+$\frac{1}{y}$）=16+1+$\frac{16y}{x}$+$\frac{x}{y}$≥17+2$\sqrt{\frac{16y}{x}•\frac{x}{y}}$=25，当且仅当x=4y时成立．
则x+y的最小值为25．
故答案为25．

点评 此题主要考查基本不等式的应用问题，题中凑基本不等式是解题的关键，有一定的技巧性，但覆盖的知识点较少，属于基础题目．

练习册系列答案
相关题目
12．已知函数f（x）=$\frac{（sin\frac{x}{2}+cos\frac{x}{2}）^{2}-1}{co{s}^{2}\frac{x}{2}-si{n}^{2}\frac{x}{2}}$，函数y=f（x）-$\sqrt{3}$在（0，+∞）上的零点按从小到大的顺序构成数列{an}（n∈N*）
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=$\frac{\frac{3}{π}{a}_{n}}{（4{n}^{2}-1）（3n-2）}$，求数列{bn}的前n项和Sn．
13．在直角三角形△ABC中，$C=\frac{π}{2}$，$|{\overrightarrow{AC}}|=3$，对平面内的任意一点M，平面内有一点D使得$3\overrightarrow{MD}=\overrightarrow{MB}+2\overrightarrow{MA}$，则$\overrightarrow{CD}•\overrightarrow{CA}$=6．
10．已知x，y为正实数，则$\frac{2x}{x+2y}+\frac{x+y}{x}$的最小值为$\frac{5}{2}$．
17．若正实数x，y满足x+2y=1，则x•y的最大值为$\frac{1}{8}$．
7．已知函数$f（x）=\frac{1-x}{ax}+lnx$在（1，+∞）上是增函数，且a＞0．
（Ⅰ）求a的取值范围；
（Ⅱ）求函数g（x）=ln（1+x）-x在[0，+∞）上的最大值；
（Ⅲ）已知a＞1，b＞0，证明：$\frac{1}{a+b}≤ln\frac{a+b}{b}＜\frac{a}{b}$．
14．在等比数列{an}中，已知a1=-1，公比q=2，则该数列前6项的和S6的值为-63．
11．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{5}$=1的右焦点与抛物线y2=12x的焦点重合，则该双曲线的焦点到其渐近线的距离等于（　　）
A．$\sqrt{5}$B．3C．5D．4$\sqrt{2}$
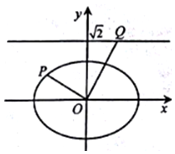12．如图，在平面直角坐标系xOy中，已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$（a＞b＞0）的离心率为$\frac{{\sqrt{2}}}{2}$，右焦点到直线x=$\frac{a^2}{c}$的距离为1．
（1）求椭圆的标准方程；
（2）若P为椭圆上的一点（点P不在y轴上），过点O作OP的垂线交直线y=$\sqrt{2}$于点Q，求$\frac{1}{{|OP{|^2}}}+\frac{1}{{|OQ{|^2}}}$的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网