题目内容
13.在直角三角形△ABC中,$C=\frac{π}{2}$,$|{\overrightarrow{AC}}|=3$,对平面内的任意一点M,平面内有一点D使得$3\overrightarrow{MD}=\overrightarrow{MB}+2\overrightarrow{MA}$,则$\overrightarrow{CD}•\overrightarrow{CA}$=6.分析 据题意,可分别以边CB,CA所在直线为x轴,y轴,建立一平面直角坐标系,得到A(0,3),并设M(x,y),D(x′,y′),B(b,0),这样根据条件$3\overrightarrow{MD}=\overrightarrow{MB}+2\overrightarrow{MA}$即可得到$\left\{\begin{array}{l}{x′=\frac{b}{3}}\\{y′=2}\end{array}\right.$,即得到$D(\frac{b}{3},2)$,进行数量积的坐标运算即可求出$\overrightarrow{CD}•\overrightarrow{CA}$的值.
解答 解:根据题意,分别以CB,CA为x,y轴,建立如图所示平面直角坐标系,则: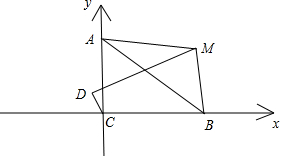
A(0,3),设M(x,y),B(b,0),D(x′,y′);
∴由$3\overrightarrow{MD}=\overrightarrow{MB}+2\overrightarrow{MA}$得:
3(x′-x,y′-y)=(b-x,-y)+2(-x,3-y);
∴$\left\{\begin{array}{l}{3x′=b}\\{3y′=6}\end{array}\right.$;
∴$\left\{\begin{array}{l}{x′=\frac{b}{3}}\\{y′=2}\end{array}\right.$;
∴$\overrightarrow{CD}•\overrightarrow{CA}=(\frac{b}{3},2)•(0,3)=6$.
故答案为:6.
点评 考查通过建立平面直角坐标系解决向量问题的方法,根据点的坐标求向量的坐标,向量坐标的数乘和数量积运算.

练习册系列答案
相关题目
18.已知实数x,y满足条件$\left\{\begin{array}{l}3x+y+3≥0\\ 2x-y+2≤0\\ x+2y-4≤0\end{array}\right.$,则z=x2+y2的取值范围为( )
| A. | [1,13] | B. | [1,4] | C. | $[{\frac{4}{5},13}]$ | D. | $[{\frac{4}{5},4}]$ |
 已知函数f(x)=6sinωxcosωx-8cos2ωx+3(ω>0),y=f(x)+1的部分图象如图所示,且f(x0)=4,则f(x0+1)=( )
已知函数f(x)=6sinωxcosωx-8cos2ωx+3(ω>0),y=f(x)+1的部分图象如图所示,且f(x0)=4,则f(x0+1)=( )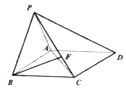 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PA=PB,PA⊥PB,F为CE上的点,且BF⊥平面PAC.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,PA=PB,PA⊥PB,F为CE上的点,且BF⊥平面PAC.