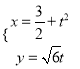Question

【题目】值域为（0，+∞）的函数是（ ）
A.
B.
C.
D.

Answer 1

【答案】B
【解析】解：A：函数定义域为{x|x≠2}，令t= ∈（﹣∞，0）∪（0，+∞），则y=5t∈（0，1）∪（1，+∞），不符合题意；B：函数定义域为R，令t=1﹣x∈R，则y= ∈（0，+∞），满足题意；
C：函数定义域为（﹣∞，0]，令t=1﹣2x∈[0，1），则y= ∈[0，1），不满足题意；
D：函数定义域为（﹣∞，0]，令t= ﹣1∈[0，+∞），则y= ∈[0，+∞），不满足题意；
故选：B
【考点精析】解答此题的关键在于理解函数的值域的相关知识，掌握求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的．