题目内容
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() ,
, ![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程,并讨论两曲线公共点的个数;
的直角坐标方程,并讨论两曲线公共点的个数;
(2)若![]() ,求由两曲线
,求由两曲线![]() 与
与![]() 交点围成的四边形面积的最大值.
交点围成的四边形面积的最大值.
【答案】(1)当![]() 或
或![]() 时,两曲线有两个公共点;
时,两曲线有两个公共点;
当![]() 时,两曲线有四个公共点;
时,两曲线有四个公共点;
当![]() 或
或![]() 时,两曲线无公共点.
时,两曲线无公共点.
(2)见解析.
【解析】试题分析:(1)利用![]() 消去参数,求得椭圆的普通方程为
消去参数,求得椭圆的普通方程为![]() ,将圆的极坐标方程两边平方,可求得圆的直角坐标方程为
,将圆的极坐标方程两边平方,可求得圆的直角坐标方程为![]() .故当
.故当![]() 或
或![]() 时,两曲线有两个公共点;当
时,两曲线有两个公共点;当![]() 时,两曲线有四个公共点;当
时,两曲线有四个公共点;当![]() 或
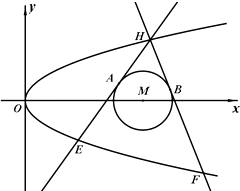
或![]() 时,两曲线无公共点.(2)根据椭圆和圆的对称性可知,四边形也关系
时,两曲线无公共点.(2)根据椭圆和圆的对称性可知,四边形也关系![]() 轴和原点对称,设四边形第一象限的点为
轴和原点对称,设四边形第一象限的点为![]() ,利用面积公式可求得最大面积为
,利用面积公式可求得最大面积为![]() .
.
试题解析:
(1)![]() ,
, ![]() .
.
当![]() 或
或![]() 时,两曲线有两个公共点;
时,两曲线有两个公共点;
当![]() 时,两曲线有四个公共点;
时,两曲线有四个公共点;
当![]() 或
或![]() 时,两曲线无公共点.
时,两曲线无公共点.
(2)由于曲线![]() 与曲线
与曲线![]() 关于
关于![]() 轴、
轴、![]() 轴以及原点对称,
轴以及原点对称,
所以四边形也关于![]() 轴、
轴、![]() 轴以及原点对称.
轴以及原点对称.
设四边形位于第一象限的点为![]() ,
,
则四边形的面积为
![]()
![]() .
.
当且仅当![]() ,即
,即![]() 时,等号成立.
时,等号成立.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目