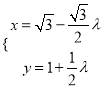题目内容
【题目】已知x，y满足不等式组 
，求
（1）z=x+2y的最大值；
（2）z=x2+y2﹣10y+25的最小值．
【答案】
（1）解：由约束条件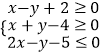 
表示的可行域如下图所示，
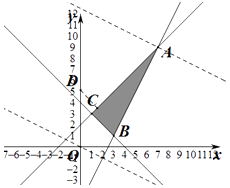
由z=x+2y，得y=﹣ 
，
平移直线y=﹣ ，由图象可知当直线y=﹣ 经过点A时，直线y=﹣ 的截距最大，此时z最大，
由 
得 
，即A（7，9），此时z=7+2×9=25
（2）解：z=x2+y2﹣10y+25=x2+（y﹣5）2，z的几何意义为点P（x，y）到点（0，5）的距离的平方；
由图知，最小值为（0，5）到直线x﹣y+2=0的距离的平方，
即d2=（ 
）2= 
．经检验，垂足在线段AC上
【解析】（1）作出不等式组对应的平面区域，利用直线平行进行求解即可．（2）z的几何意义是两点间的距离的平方，利用点到直线的距离公式进行求解即可．
练习册系列答案
习题精选系列答案
相关题目
【题目】“累积净化量
”是空气净化器质量的一个重要衡量指标，它是指空气净化从开始使用到净化效率为50%时对颗粒物的累积净化量，以克表示，根据
《空气净化器》国家标准，对空气净化器的累计净化量有如下等级划分：
累积净化量（克） |
|
|
| 12以上 |
等级 |
|
|
|
|
为了了解一批空气净化器（共5000台）的质量，随机抽取
台机器作为样本进行估计，已知这台机器的累积净化量都分布在区间
中，按照
、
、
、
、
均匀分组，其中累积净化量在的所有数据有：4.5,4.6,5.2,5.3,5.7和5.9，并绘制了频率分布直方图，如图所示：
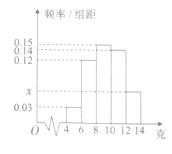
（1）求的值及频率分布直方图中
的值；
（2）以样本估计总体，试估计这批空气净化器（共5000台）中等级为
的空气净化器有多少台？
（3）从累积净化量在的样本中随机抽取2台，求恰好有1台等级为的概率.
