题目内容
已知f（x）=tanx+cos（x+m）为奇函数，且m满足不等式m2-3m-10＜0，则m的值为 ．
【答案】分析：根据定义在R奇函数当x=0时的函数值为0，解出m=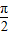
+kπ（k∈Z），再解出不等式m2-3m-10＜0的解集，可得m∈（-2，5），分别取k=-1、0、1，得符合题意的3个m的值．
解答：解：∵定义在R上的函数f（x）=tanx+cos（x+m）为奇函数，
∴f（0）=tan0+cosm=0，解之得m=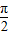
+kπ，（k∈Z）
又∵m满足不等式m2-3m-10＜0，即m∈（-2，5）
∴分别取k=-1、0、1，得m=-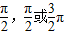
符合题意
故答案为：-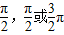
点评：本题给出含有参数m的函数为奇函数，求参数m满足的条件，着重考查了一元二次不等式的解法、函数的奇偶性和三角函数的图象与性质等知识，属于基础题．
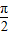+kπ（k∈Z），再解出不等式m2-3m-10＜0的解集，可得m∈（-2，5），分别取k=-1、0、1，得符合题意的3个m的值．解答：解：∵定义在R上的函数f（x）=tanx+cos（x+m）为奇函数，
∴f（0）=tan0+cosm=0，解之得m=
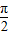+kπ，（k∈Z）又∵m满足不等式m2-3m-10＜0，即m∈（-2，5）
∴分别取k=-1、0、1，得m=-
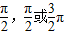符合题意故答案为：-
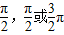
点评：本题给出含有参数m的函数为奇函数，求参数m满足的条件，着重考查了一元二次不等式的解法、函数的奇偶性和三角函数的图象与性质等知识，属于基础题．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
，tanθ＞0，则cosθ=
；
既是奇函数又是偶函数；