题目内容
下列说法：①若sinθ=-
，tanθ＞0，则cosθ=
；②若f（x）=ax2+（2a+b）x+2（其中x∈[2a-1，a+4]）是偶函数，则实数b=2；
③f（x）=
既是奇函数又是偶函数；④已知f（x）是定义在R上的奇函数，若当x∈[0，+∞）时，f（x）=x（1+x），则当x∈R时，f（x）=x（1+|x|）．其中所有正确说法的序号是 ．
【答案】分析：①根据sinθ=-
，tanθ＞0，则必有cosθ＜0，可判定真假；②根据函数的奇偶性可知区间[2a-1，a+4]应关于原点对称可求出a的值，再根据f（x）是偶函数求出b的值，可判定真假；③先化简f（x）可判定真假；④先求出x∈（-∞，0）时的函数解析式从而求出x∈R时的解析式，可判定真假．
解答：解：①中必有cosθ＜0，显然错误；
②依条件知，区间[2a-1，a+4]应关于原点对称，∴（2a-1）+（a+4）=0，得a=-1；又f（x）是偶函数，则2a+b=0，故b=2；
③中定义域是{x|x=±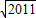
}，且化简得f（x）=0，故是既奇又偶的函数；
④中当x∈（-∞，0）时，-x∈（0，+∞），则f（-x）=-x（1-x），又f（-x）=-f（x），故f（x）=x（1-x）（x＜0），综合可得f（x）=x（1+|x|），故正确．
故答案为：②③④
点评：本题主要考查了命题的真假判断与应用，同时考查了函数奇偶性的判定和三角不等式的解法，属于基础题．
，tanθ＞0，则必有cosθ＜0，可判定真假；②根据函数的奇偶性可知区间[2a-1，a+4]应关于原点对称可求出a的值，再根据f（x）是偶函数求出b的值，可判定真假；③先化简f（x）可判定真假；④先求出x∈（-∞，0）时的函数解析式从而求出x∈R时的解析式，可判定真假．解答：解：①中必有cosθ＜0，显然错误；
②依条件知，区间[2a-1，a+4]应关于原点对称，∴（2a-1）+（a+4）=0，得a=-1；又f（x）是偶函数，则2a+b=0，故b=2；
③中定义域是{x|x=±
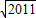}，且化简得f（x）=0，故是既奇又偶的函数；④中当x∈（-∞，0）时，-x∈（0，+∞），则f（-x）=-x（1-x），又f（-x）=-f（x），故f（x）=x（1-x）（x＜0），综合可得f（x）=x（1+|x|），故正确．
故答案为：②③④
点评：本题主要考查了命题的真假判断与应用，同时考查了函数奇偶性的判定和三角不等式的解法，属于基础题．
练习册系列答案
相关题目
，则sin α=
”的否命题是假命题；
+2kπ（k∈Z）”是“函数y=sin（2x+φ）为偶函数”的充要条件；
），使sin x+cos x=
”，命题q：“在△ABC中，若sin A＞sin B，则A＞B”，那么命题￢p∧q为真命题．