题目内容

已知p:函数y=x2+mx+1在(-1,+∞)上单调递增,q:函数y=4x2+4(m-2)x+1大于零恒成立.

若p或q为真,p且q为假,求m的取值范围.

解:若函数y=x2+mx+1在(-1,+∞)上单调递增,则≤-1,∴m≥2,

即p:m≥2;若函数y=4x2+4(m-2)x+1恒大于零,

则Δ=16(m-2)2-16＜0,

解得1＜m＜3,即q:1＜m＜3.

因为p或q为真,p且q为假,所以p、q一真一假.

当p真q假时,由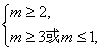得m≥3.

当p假q真时,由得1＜m＜2.

综上,m的取值范围是{m|m≥3或1＜m＜2}.

练习册系列答案
相关题目
已知幂函数y=xm2-2m-3(m∈N+)的图象与x轴，y轴无交点且关于原点对称，又有函数f（x）=x2-alnx+m-2在（1，2]上是增函数，g（x）=x-a
x
在（0，1）上为减函数．
①求a的值；
②若
1
p(x)
=2f′(x)-2x+
5
x
+1，数列{an}满足a1=1，an+1=p（an），（n∈N+），数列{bn}，满足bn=
1
2
anan+13n，sn=b1+b2+b3+…+bn，求数列{an}的通项公式an和sn．
③设h(x)=f′(x)-g(x)-2
x
+
3
x
，试比较[h（x）]n+2与h（xn）+2n的大小（n∈N+），并说明理由．
已知奇函数f（x）=ax3+bx2+cx（a≠0）在x=1处取得极大值2．
（1）求函数y=f（x）的解析式；
（2）对于区间[-2，2]上任意两个自变量的值x1，x2都有|f（x1）-f（x2）|≤c，求实数c的最小值；
（3）若关于p的一元二次方程p2-2mp+4=0两个根均大于1，求函数g(x)=
f(x)x
+mlnx的单调区间．
选修4-4：坐标系与参数方程：
（1）已知二次函数y=x2-2xsecα+
2+sin2α2cos2α
，（α为参数，cosα≠0）求证此抛物线顶点的轨迹是双曲线．
（2）长为2a的线段两端点分别在直角坐标轴上移动，从原点向该线段作垂线，垂足为P，求P的轨迹的极坐标方程．
已知命题P“函数y=x2+mx+1的图象与x轴负半轴有两个不同交点”；命题Q“不等式|x-1|≤(m-1)(m-3)的解集为空集”.若命题P或Q为真,P且Q为假,求实数m的取值范围.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网