Question

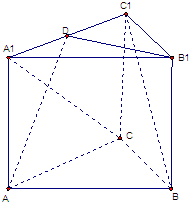（2008•南京二模）如图，已知正三棱柱ABC-A₁B₁C₁中，AB=

2

AA1，点D为A₁C₁的中点．
求证：
（1）BC₁∥平面AB₁D；
（2）A₁C⊥平面AB₁D．

Answer 1

分析：（1）连结A₁B，设A₁B∩AB₁=O，连结OD．利用三角形中位线定理证出OD∥BC₁，再根据线面平行的判定定理，即可证出BC₁∥平面AB₁D；
（2）利用线面垂直的判定与性质，证出B₁D⊥平面AA₁C₁C，从而得到B₁D⊥A₁C．矩形AA₁C₁C中，根据AC=

2

AA1利用直角三角形相似证出A₁C⊥AD，最后利用线面垂直判定定理即可证出A₁C⊥平面AB₁D．

解答：解：（1）连结A₁B，设A₁B∩AB₁=O，连结OD
∵△A₁BC₁中，A₁D=DC₁，A₁O=OB
∴OD∥BC₁
∵OD?平面AB₁D，BC₁?平面AB₁D，
∴BC₁∥平面AB₁D；
（2）在正三棱柱ABC-A₁B₁C₁中，AA₁⊥平面A₁B₁C₁，
∵B₁D?平面A₁B₁C₁，∴B₁D⊥AA₁，
∵B₁D是正三角形A₁B₁C₁的中线，可得B₁D⊥A₁C₁
∴结合AA₁∩A₁C₁=A₁，得B₁D⊥平面AA₁C₁C
∵A₁C?平面AA₁C₁C，∴B₁D⊥A₁C，
∵AB=

2

AA1，∴

A1D

AA1

=

AA1

AC

=

2

2

∵∠DA₁A=∠A₁AC=Rt∠
∴△DA₁A∽△A₁AC，可得∠ADA₁=∠CA₁A=90°-∠DA₁C
因此，∠ADA₁+∠DA₁C=90°，从而A₁C⊥AD
∵B₁D、AD是平面AB₁D内的相交直线，
∴A₁C⊥平面AB₁D．

点评：本题在特殊正三棱柱中证明线面平行和线面垂直，着重考查了线面平行判定定理、线面垂直的判定与性质和正三棱柱的性质等知识，属于中档题．