题目内容
（2008•南京二模）已知复数z1=a+i，z2=1-i，若z1•z2是纯虚数，则实数a的值为
-1
-1
．分析：根据 z1•z2=a+1+（1-a）i，且z1•z2是纯虚数，可得a+1=0，由此求得实数a的值．
解答：解：∵z1•z2=（a+i）（1-i）=a+1+（1-a）i，且z1•z2是纯虚数，
故有 a+1=0，∴a=-1．
故答案为：-1．
故有 a+1=0，∴a=-1．
故答案为：-1．
点评：本题主要考查复数的基本概念，两个复数代数形式的乘法，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
（2008•南京二模）如图，半圆的直径AB=2，O为圆心，C为半圆上不同于A，B的任意一点，若P为半径OC上的动点，则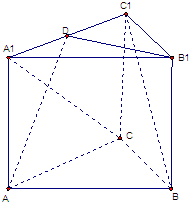
（2008•南京二模）如图，已知正三棱柱ABC-A1B1C1中，AB=