题目内容
7．已知M为抛物线y2=4x上一动点，F为这条抛物线的焦点，有一个定点A（3，2），则|MA|+|MF|的最小值=4．分析 设点M在准线上的射影为D，则根据抛物线的定义可知|MF|=|MD|进而把问题转化为求|MA|+|MD|取得最小，进而可推断出当D，M，A三点共线时|MA|+|MD|最小，答案可得．
解答 解：设点M在准线上的射影为D，则根据抛物线的定义可知|MF|=|MD|，
∴要求|MA|+|MF|取得最小值，即求|MA|+|MD|取得最小，
当D，M，A三点共线时|MA|+|MD|最小，为3-（-1）=4．
故答案为：4．
点评 本题考查抛物线的定义、标准方程，以及简单性质的应用，判断当D，M，A三点共线时|MA|+|MD|最小是解题的关键．
练习册系列答案
相关题目
18．已知集合A={x|y=log2（4-x2）}，B={y|y=2x+1}，则A∩B=（ ）
| A． | ∅ | B． | （1，3） | C． | （1，+∞） | D． | （1，2） |
15．已知命题p：?m∈R，使得函数f（x）=x2+（m-1）x2-2是奇函数，命题q：向量$\overrightarrow{a}$=（x1，y1），$\overrightarrow{b}$=（x2，y2），则“$\frac{{x}_{1}}{{x}_{2}}$=$\frac{{y}_{1}}{{y}_{2}}$”是：“$\overrightarrow{a}$$∥\overrightarrow{b}$”的充要条件，则下列命题为真命题的是（ ）
| A． | p∧q | B． | （￢p）∧q | C． | p∧（￢q） | D． | （￢p）∧（￢q） |
2．设M是圆P：（x+5）2+y2=36上一动点，点Q的坐标为（5，0），若线段MQ的垂直平分线交直线PM于点N，则点N的轨迹方程为（ ）
| A． | $\frac{x^2}{25}+\frac{y^2}{9}=1$ | B． | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | C． | $\frac{x^2}{25}-\frac{y^2}{9}=1$ | D． | $\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=1$ |
19．复数i-i2在复平面内表示的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
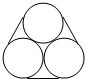李师傅在建材商店购买了三根外围直径都为10cm的钢管，为了便于携带，他将三根钢管用铁丝紧紧捆住，截面如图所示，则铁丝捆扎一圈的长度为30+10πcm．