题目内容
2.设M是圆P:(x+5)2+y2=36上一动点,点Q的坐标为(5,0),若线段MQ的垂直平分线交直线PM于点N,则点N的轨迹方程为( )| A. | $\frac{x^2}{25}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | C. | $\frac{x^2}{25}-\frac{y^2}{9}=1$ | D. | $\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=1$ |
分析 由已知作出图象,结合图象得|NQ|-|NP|=6,Q(5,0),P(-5,0),|PQ|=10>6,由此能求出点N的轨迹.
解答 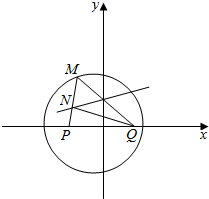 解:∵M是圆P:(x+5)2+y2=36上一动点,点Q的坐标为(5,0),线段MQ的垂直平分线交直线PM于点N,
解:∵M是圆P:(x+5)2+y2=36上一动点,点Q的坐标为(5,0),线段MQ的垂直平分线交直线PM于点N,
∴|MN|=|NQ|,|NQ|-|NP|=|MP|,
∵M是圆P:(x+5)2+y2=36上一动点,点Q的坐标为(5,0),
∴|MP|=6,∴|NQ|-|NP|=6,
∵Q(5,0),∴P(-5,0),|PQ|=10>6,
∴点N的轨迹为双曲线,a=3,c=5,b=4,
∴点N的轨迹方程为$\frac{{x}^{2}}{9}-\frac{{y}^{2}}{16}=1$.
故选:D.
点评 本题主要考查了轨迹方程的问题,解题的关键是利用了双曲线的定义求得轨迹方程.

练习册系列答案
相关题目
18.函数y=$\sqrt{k{x}^{2}-6kx+k+8}$的定义域为一切实数,则k的取值范围是( )
| A. | k>0或k≤-9 | B. | k≥1 | C. | -9≤k≤1 | D. | 0≤k≤1 |
13.已知函数$f(x)=\left\{\begin{array}{l}1,\;\;-1≤x≤0\\ \frac{1}{x},\;\;x>0\end{array}\right.$,则使方程x+f(x)=m有解的实数m的取值范围是( )
| A. | (-∞,0)∪(1,2) | B. | [0,+∞) | C. | (-∞,1]∪[2,+∞) | D. | [0,1]∪[2,+∞) |
17.已知命题p:?x∈R,ex+x3+2x2+4≠0,则?p为( )
| A. | ?x0∈R,使得lnx0+x03+2x02+4=0 | B. | ?x0∈R,使得ex0+x03+2x02+4≠0 | ||
| C. | ?x∈R,使得ex+x3+2x2+4=0 | D. | ?x0∈R,使得ex0+x03+2x02+4=0 |
14.“$?{x_0}∈{C_R}Q,x_0^2∈Q$”的否定是( )
| A. | $?{x_0}∉{C_R}Q,x_0^2∈Q$ | B. | $?{x_0}∈{C_R}Q,x_0^2∉Q$ | ||
| C. | $?{x_0}∈{C_R}Q,x_0^2∈Q$ | D. | $?{x_0}∈{C_R}Q,x_0^2∉Q$ |
11.已知命题P:?x∈R,3x2+1>0,则¬p为( )
| A. | ?x∈R,3x2+1≤0 | B. | ?x∈R,3x2+1≤0 | C. | ?x∈R,3x2+1<0 | D. | ?x∈R,3x2+1<0 |
12.已知α>0且a≠1,函数f(x)=$\left\{\begin{array}{l}{(a-1)x+3a-4,(x≤0)}\\{{a}^{x},(x>0)}\end{array}\right.$满足对任意实数x1≠x2,都有x1f(x1)+x2f(x2)>x1f(x2)+x2f(x1)成立,则a的取值范围是( )
| A. | $(1,\frac{5}{3}]$ | B. | (0,1) | C. | (1,+∞) | D. | $[\frac{5}{3},2)$ |