题目内容
15.(Ⅰ)设函数f(x)=$\left\{{\begin{array}{l}{{{log}_{\frac{1}{2}}}x}&{x>0}\\{x+6}&{x≤0}\end{array}}$,计算f(f(-4))的值;(Ⅱ)计算:log525+lg$\frac{1}{100}+ln\sqrt{e}+{2^{{{log}_2}1}}$;
(Ⅲ)计算:${(\frac{9}{16})^{0.5}}+{(-3)^{-1}}÷{0.75^{-2}}-{(2\frac{10}{27})^{-\;\frac{2}{3}}}$.
分析 (Ⅰ)利用函数f(x)=$\left\{{\begin{array}{l}{{{log}_{\frac{1}{2}}}x}&{x>0}\\{x+6}&{x≤0}\end{array}}$,直接计算f(f(-4))的值;
(Ⅱ)直接利用对数运算法则化简求解log525+lg$\frac{1}{100}+ln\sqrt{e}+{2^{{{log}_2}1}}$;
(Ⅲ)利用有理指数幂的运算法则化简求解${(\frac{9}{16})^{0.5}}+{(-3)^{-1}}÷{0.75^{-2}}-{(2\frac{10}{27})^{-\;\frac{2}{3}}}$.
解答 解:(Ⅰ)因为-4<0,所以f(-4)=-4+6=2>0----------------(1分)
所以,$f(f(-4))=f(2)={log_{\frac{1}{2}}}2=-1$.---------------(3分)
(Ⅱ)${log_5}25+lg\frac{1}{100}+ln\sqrt{e}+{2^{{{log}_2}1}}$=$2+(-2)+\frac{1}{2}+1=\frac{3}{2}$(每一项(1分)结论1分)--------(8分)
(Ⅲ)${(\frac{9}{16})^{0.5}}+{(-3)^{-1}}÷{0.75^{-2}}-{(2\frac{10}{27})^{-\;\frac{2}{3}}}$=$\frac{3}{4}-\frac{1}{3}÷\frac{16}{9}-\frac{9}{16}$=$\frac{3}{4}-\frac{3}{16}-\frac{9}{16}=0$; (每一项(1分)结论1分)---------------(13分)
点评 本题考查分段函数以及有理指数幂,对数运算法则的应用,考查计算能力.

| A. | $\sqrt{7}$ | B. | 3 | C. | $\frac{1}{3}$ | D. | $\frac{{\sqrt{7}}}{7}$ |
| A. | an=n-1 | B. | an=n | C. | an=n+1 | D. | an=n2 |
| x | 0 | 1 | 2 | 3 | 4 |
| y | 2.2 | 4.3 | t | 4.8 | 6.7 |
| A. | 4.7 | B. | 4.6 | C. | 4.5 | D. | 4.4 |
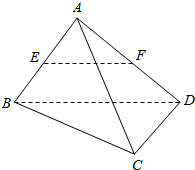 在空间四边形ABCD中,E,F分别是AB,AD的中点
在空间四边形ABCD中,E,F分别是AB,AD的中点