题目内容
下列结论中：
①函数y＝x(1－2x)(x>0)有最大值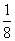
；
②函数y＝2－3x－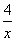
(x<0)有最大值2－4
；
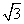③若a>0，则(1＋a)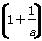
≥4.
正确结论的序号是________．
①③
练习册系列答案
名校课堂系列答案
相关题目
名校课堂系列答案题目内容
下列结论中：
①函数y＝x(1－2x)(x>0)有最大值；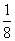
②函数y＝2－3x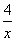－(x<0)有最大值2－4；
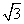③若a>0，则(1＋a)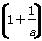≥4.
正确结论的序号是________．
①③
名校课堂系列答案
的图象大致是( )
≤2f(1)，那么t的取值范围是________．
＝0，则k＝( )
B.
C.
D．2
，P(ξ＝x2)＝
，且x1<x2，又已知E(ξ)＝
，D(ξ)＝
，则x1＋x2的值为( )
B.
C．3 D.
＋7.若“∃x∈[0，＋∞)，f(x)＜a＋1”是假命题，则a的取值范围为________．