题目内容
在直角坐标系中,角φ、2x的终边分别与单位圆(以原点O为圆心)交于A、B两点,函数 ,若
,若 对x∈R恒成立.
对x∈R恒成立.(1)求函数f(x)的解析式;
(2)求函数f(x)的对称轴与单调递减区间.
【答案】分析:(1)利用向量的数量积公式,结合 对x∈R恒成立,确定函数的解析式;
对x∈R恒成立,确定函数的解析式;
(2)利用余弦函数的性质,即可求函数f(x)的对称轴与单调递减区间.
解答:解:(1)∵角φ、2x的终边分别与单位圆(以原点O为圆心)交于A、B两点,
∴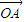 =(cosφ,sinφ),
=(cosφ,sinφ), =(cos2x,sin2x)
=(cos2x,sin2x)
∴ =cosφcos2x+sinφsin2x=cos(2x-φ)
=cosφcos2x+sinφsin2x=cos(2x-φ)
∵ 对x∈R恒成立,
对x∈R恒成立,
∴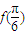 =1,即cos(2×
=1,即cos(2× -φ)=1
-φ)=1
∴
∴φ= ,k∈Z
,k∈Z
∴f(x)=cos[2x-(2kx+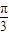 )]=cos(2x-
)]=cos(2x- ),
),
即函数f(x)的解析式为f(x)=cos(2x-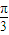 )
)
(2)由(1)知,f(x)=cos(2x- ),
),
令2x- =kπ,k∈Z,得x=
=kπ,k∈Z,得x= ,k∈Z,
,k∈Z,
∴f(x)的对称轴为x= ,k∈Z,
,k∈Z,
∵2kπ ,k∈Z,
,k∈Z,
kπ ,k∈Z,
,k∈Z,
故函数f(x)的单调递减区间为[ ],k∈Z,
],k∈Z,
点评:本题考查向量知识的运用,考查三角函数性质,考查学生计算能力,属于中档题.
 对x∈R恒成立,确定函数的解析式;
对x∈R恒成立,确定函数的解析式;(2)利用余弦函数的性质,即可求函数f(x)的对称轴与单调递减区间.
解答:解:(1)∵角φ、2x的终边分别与单位圆(以原点O为圆心)交于A、B两点,
∴
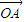 =(cosφ,sinφ),
=(cosφ,sinφ), =(cos2x,sin2x)
=(cos2x,sin2x)∴
 =cosφcos2x+sinφsin2x=cos(2x-φ)
=cosφcos2x+sinφsin2x=cos(2x-φ)∵
 对x∈R恒成立,
对x∈R恒成立,∴
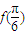 =1,即cos(2×
=1,即cos(2× -φ)=1
-φ)=1∴

∴φ=
 ,k∈Z
,k∈Z∴f(x)=cos[2x-(2kx+
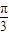 )]=cos(2x-
)]=cos(2x- ),
),即函数f(x)的解析式为f(x)=cos(2x-
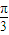 )
)(2)由(1)知,f(x)=cos(2x-
 ),
),令2x-
 =kπ,k∈Z,得x=
=kπ,k∈Z,得x= ,k∈Z,
,k∈Z,∴f(x)的对称轴为x=
 ,k∈Z,
,k∈Z,∵2kπ
 ,k∈Z,
,k∈Z,kπ
 ,k∈Z,
,k∈Z,故函数f(x)的单调递减区间为[
 ],k∈Z,
],k∈Z,点评:本题考查向量知识的运用,考查三角函数性质,考查学生计算能力,属于中档题.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 中,角
中,角 的顶点是原点,始边与
的顶点是原点,始边与 轴正半轴重合,终边交单位圆于点
轴正半轴重合,终边交单位圆于点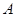 ,且
,且 .将角
.将角 ,交单位圆于点
,交单位圆于点 .记
.记 .
.
 ,求
,求 ;
; 作
作 .记△
.记△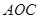 的面积为
的面积为 ,△
,△ 的面积为
的面积为 .若
.若 ,求角
,求角 中,角
中,角 的顶点为坐标原点,始边在
的顶点为坐标原点,始边在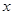 轴的正半轴上,当角
轴的正半轴上,当角 :
: =3
=3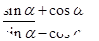 的值; (2)
的值; (2) 的值.
的值.