题目内容
11.已知平行直线l1:2x+y-1=0,l2:2x+y+1=0,则l1,l2的距离$\frac{2\sqrt{5}}{5}$;点(0,2)到直线l1的距离$\frac{\sqrt{5}}{5}$.分析 直接利用两条平行直线间的距离公式,点到直线的距离公式运算求得结果.
解答 解:∵l1:2x+y-1=0,l2:2x+y+1=0,
∴l1,l2的距离d=$\frac{|1-(-1)|}{\sqrt{4+1}}$=$\frac{2\sqrt{5}}{5}$;
点(0,2)到直线l1的距离d=$\frac{|2-1|}{\sqrt{5}}$=$\frac{{\sqrt{5}}}{5}$;
故答案为:$\frac{2\sqrt{5}}{5}$,$\frac{\sqrt{5}}{5}$.
点评 本题主要考查两条平行直线间的距离公式以及点到直线的距离公式的应用,注意未知数的系数相同,属于基础题.

练习册系列答案
相关题目
20. 如图,一个正六角星薄片(其对称轴与水面垂直)匀速地升出水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(t)的图象大致为( )
如图,一个正六角星薄片(其对称轴与水面垂直)匀速地升出水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(t)的图象大致为( )
 如图,一个正六角星薄片(其对称轴与水面垂直)匀速地升出水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(t)的图象大致为( )
如图,一个正六角星薄片(其对称轴与水面垂直)匀速地升出水面,直到全部露出水面为止,记时刻t薄片露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S'(t)的图象大致为( )| A. | 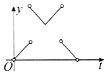 | B. |  | C. | 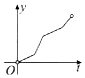 | D. | 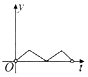 |
1.曲线y=x3+2x+1在点P(1,4)处的切线与y轴交点的纵坐标是( )
| A. | -9 | B. | -3 | C. | -1 | D. | 3 |