题目内容
6.已知x>0,y>0,且x+y=1,求:(1)x2+y2的最小值;
(2)$\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{xy}$的最小值.
分析 (1)利用重要不等式求解表达式的最小值即可.
(2)利用已知条件求出xy的最值,然后化简所求的表达式,利用基本不等式求解最小值即可.
解答 (12分)
解:(1)${x^2}+{y^2}=\frac{{{x^2}+{y^2}+{x^2}+{y^2}}}{2}≥\frac{{{x^2}+{y^2}+2xy}}{2}=\frac{{{{({x+y})}^2}}}{2}=\frac{1}{2}$,当且仅当x=y=$\frac{1}{2}$.表达式取得最小值$\frac{1}{2}$.
(2)∵x+y=1,∴$xy≤{({\frac{x+y}{2}})^2}=\frac{1}{4}$,∴$\frac{1}{xy}≥4$.∴$\frac{1}{x}$+$\frac{1}{y}$+$\frac{1}{xy}$=$\frac{x+y+1}{xy}=\frac{2}{xy}≥8$.当且仅当x=y=$\frac{1}{2}$.表达式的最小值为:6.
点评 本题考查基本不等式在最值中的应用,考查计算能力.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
3.已知过抛物线y2=4x的焦点F作直线l交抛物线于A,B两点,若$\overrightarrow{BF}$=2$\overrightarrow{FA}$,则点A的横坐标为( )
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
14.函数y=sinx(cosx-$\sqrt{3}$sinx)(0≤x≤$\frac{π}{2}$)的值域为( )
| A. | [$\sqrt{3}$,1+$\frac{\sqrt{3}}{2}$] | B. | [-$\frac{\sqrt{3}}{2}$,1-$\frac{\sqrt{3}}{2}$] | C. | [0,1] | D. | [-$\sqrt{3}$,1-$\frac{\sqrt{3}}{2}$] |

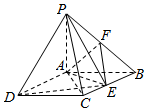 如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动.
如图,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=$\sqrt{3}$,点F是PB的中点,点E在边BC上移动.