题目内容
19.已知函数f(x)=loga(2-ax)在区间[1,3]上是增函数,则实数a的取值范围是0<a<$\frac{2}{3}$.分析 根据函数t=2-ax在[1,3]上为减函数,函数f(x)=loga(2-ax),x∈[1,3]上为增函数,可得$\left\{\begin{array}{l}0<a<1\\ 2-3a>0\end{array}\right.$,由此求得a的范围
解答 解:对于函数f(x)=loga(2-ax),由于a>0,a≠1,
故函数t=2-ax在[1,3]上为减函数.
再根据函数f(x)=loga(2-ax),x∈[1,3]上为增函数,
可得$\left\{\begin{array}{l}0<a<1\\ 2-3a>0\end{array}\right.$,
解得:0<a<$\frac{2}{3}$,
故答案为:0<a<$\frac{2}{3}$
点评 本题主要考查复合函数的单调性,对数函数的性质应用,体现了转化的数学思想,属于基础题.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
4.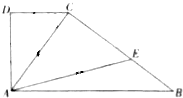 如图所示直角梯形ABCD中,∠BAD=∠ADC=90°,∠ACD=60°,AB=3DC=3,若线段BC上存在点E,使得AC、AE、AB成等比数列,则$\frac{CE}{CB}$等于( )
如图所示直角梯形ABCD中,∠BAD=∠ADC=90°,∠ACD=60°,AB=3DC=3,若线段BC上存在点E,使得AC、AE、AB成等比数列,则$\frac{CE}{CB}$等于( )
 如图所示直角梯形ABCD中,∠BAD=∠ADC=90°,∠ACD=60°,AB=3DC=3,若线段BC上存在点E,使得AC、AE、AB成等比数列,则$\frac{CE}{CB}$等于( )
如图所示直角梯形ABCD中,∠BAD=∠ADC=90°,∠ACD=60°,AB=3DC=3,若线段BC上存在点E,使得AC、AE、AB成等比数列,则$\frac{CE}{CB}$等于( )| A. | $\frac{1+\sqrt{15}}{7}$ | B. | $\frac{6-\sqrt{15}}{7}$ | C. | $\frac{\sqrt{87}-9}{7}$ | D. | $\frac{18-\sqrt{87}}{7}$ |
9.设曲线y=3x-ln(x+a)在点(0,0)处的切线方程为y=2x,则a=( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
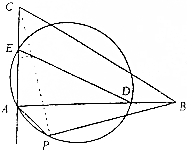 如图,△BC中,AB>AC,点D、E分别在边AB、AC上,且BD=CE,∠BAC的外角平分线与△ADE的外接圆交于A、P两点.求证:A、P、B、C四点共圆.
如图,△BC中,AB>AC,点D、E分别在边AB、AC上,且BD=CE,∠BAC的外角平分线与△ADE的外接圆交于A、P两点.求证:A、P、B、C四点共圆.