题目内容
已知
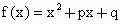 ,求证:|f(1)|,|f(2)|,|f(3)|中至少有一个不小于
,求证:|f(1)|,|f(2)|,|f(3)|中至少有一个不小于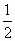 .
.
答案:略
解析:
解析:
|
证明:假设 |f(1)|,|f(2)|,|f(3)|都小于 , ,
则 |f(1)|+2|f(2)|+|f(3)|<2,则 |f(1)|+2|f(2)|+|f(3)|≥|f(1)+f(3)-2f(2)|=|(1 +p+q)+(9+3p+q)-(8+4p+2q)|=2,这与假设相矛盾,从而假设不成立,所以原命题成立,即 |f(1)|,|f(2)|,|f(3)|中至少有一个不小于 . . |

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
 ,
,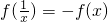 .
.
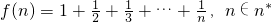 ,求证:
,求证: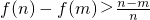 ;
;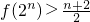 ;
;