题目内容
已知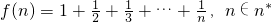 ,求证:
,求证:
(1)当m<n(m∈N*)时,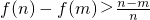 ;
;
(2)当n>1时,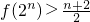 ;
;
(3)对于任意给定的正数M,总能找到一个正整数N0,使得当n>N0时,有f(n)>M.
证明:(1)当m<n时,
f(n)-f(m)= ≥
≥ =
= .
.
(2)当n>1时,

 ;
;
(3)∵ ,
,
∴f(n)在N*上单调递增.
由(2)可知,当n>1时, .对任意给定的正数M,设M0是比M大的最小正整数,
.对任意给定的正数M,设M0是比M大的最小正整数,
取 ,则当n>N0时,
,则当n>N0时, .
.
分析:(1)当m<n时,考察f(n)与(m)的差f(n)-f(m),结合放缩法即可证得;
(2)当n>1时, 利用放缩法结合等比数列的求和公式即得结论;
利用放缩法结合等比数列的求和公式即得结论;
(3)由于 ,得出f(n)在N*上单调递增.由(2)可知,当n>1时,
,得出f(n)在N*上单调递增.由(2)可知,当n>1时, .对任意给定的正数M,设M0是比M大的最小正整数,取
.对任意给定的正数M,设M0是比M大的最小正整数,取 ,则当n>N0时,有f(n)>M.
,则当n>N0时,有f(n)>M.
点评:本小题主要考查综合法与分析法、不等式的证法等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.
f(n)-f(m)=
 ≥
≥ =
= .
.(2)当n>1时,

 ;
;(3)∵
 ,
,∴f(n)在N*上单调递增.
由(2)可知,当n>1时,
 .对任意给定的正数M,设M0是比M大的最小正整数,
.对任意给定的正数M,设M0是比M大的最小正整数,取
 ,则当n>N0时,
,则当n>N0时, .
.分析:(1)当m<n时,考察f(n)与(m)的差f(n)-f(m),结合放缩法即可证得;
(2)当n>1时,
 利用放缩法结合等比数列的求和公式即得结论;
利用放缩法结合等比数列的求和公式即得结论;(3)由于
 ,得出f(n)在N*上单调递增.由(2)可知,当n>1时,
,得出f(n)在N*上单调递增.由(2)可知,当n>1时, .对任意给定的正数M,设M0是比M大的最小正整数,取
.对任意给定的正数M,设M0是比M大的最小正整数,取 ,则当n>N0时,有f(n)>M.
,则当n>N0时,有f(n)>M.点评:本小题主要考查综合法与分析法、不等式的证法等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
相关题目
 ,复数
,复数 ,
, .
. 取何值时,
取何值时, 是实数;
是实数; .
.