题目内容
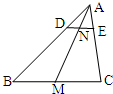△ABC中，| AD |
| 1 |
| 4 |
| AB |
| AB |
| a |
| AC |
| b |
（1）试用
| a |
| b |
| DN |
（2）若|
| a |
| b |
| |DN |
分析：（1）由于DE∥BC又AM为中线，根据三角形中位线定理得
=
，又
=
从而有：
=
，再利用向量的减法的三角形法则得到
=
-
即可得到结论；
（2）由（1）知
=
(
-
)，由于|
|=4，|
|=2，∠BAC=600根据向量模的平方等于向量的平方得|
|2，从而求得
|．
| DN |
| 1 |
| 2 |
| DE |
| AD |
| 1 |
| 4 |
| AB |
| DN |
| 1 |
| 8 |
| BC |
| BC |
| AC |
| AB |
（2）由（1）知
| DN |
| 1 |
| 8 |
| b |
| a |
| a |
| b |
| DN |
| |DN |
解答：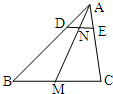
解：（1）∵DE∥BC又AM为中线，
∴
=
…（1分）
又
=
，
∴
=
∴
=
…（4分）
而
=
-
且
=
，
=
，
∴
=
(
-
)．…（6分）
（2）由（1）知
=
(
-
)
∵|
|=4，|
|=2，∠BAC=600
∴|
|2=
(
2+
2-2
•
)=
(4+16-8)=
…(10分)
∴
|=
．
解：（1）∵DE∥BC又AM为中线，∴
| DN |
| 1 |
| 2 |
| DE |
又
| AD |
| 1 |
| 4 |
| AB |
∴
| DE |
| 1 |
| 4 |
| BC |
∴
| DN |
| 1 |
| 8 |
| BC |
而
| BC |
| AC |
| AB |
| AB |
| a |
| AC |
| b |
∴
| DN |
| 1 |
| 8 |
| b |
| a |
（2）由（1）知
| DN |
| 1 |
| 8 |
| b |
| a |
∵|
| a |
| b |
∴|
| DN |
| 1 |
| 64 |
| b |
| a |
| b |
| a |
| 1 |
| 64 |
| 3 |
| 16 |
∴
| |DN |
| ||
| 4 |
点评：本题考查向量的几何表示，三角形相似的性质，向量的共线定理，向量的模，平面向量基本定理，体现了数形结合的数学思想．
练习册系列答案
相关题目
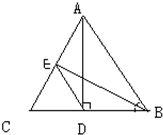在△ABC中，AD是BC边上的高，垂足为D点．BE是∠ABC的角平分线，并交AC于E点．若BC=6，CA=7，AB=8．
如图，在△ABC中，AD⊥BC，
如图所示，已知△ABC中，AD是BC边上的中线，E是AD的中点，BE的延长线交AC于点F，则AF：AC=