题目内容
设各项均为正数的数列
的前n项和为Sn，已知
，且
对一切
都成立．
（1）若λ = 1，求数列的通项公式；
（2）求λ的值，使数列是等差数列．
(1)
；(2)
．
【解析】
∴当
时，
．②
② - ①，得
， ∴
（）． ………………… 6分
所以λ = 0时，数列是等差数列． ………………… 16分
考点：递推公式，累乘法，
与
的关系，等差数列．
练习册系列答案
名校课堂系列答案
相关题目
π，
，相应输出的y分别为y1，y2，则y1，y2的大小关系是( )
，则
= ； 
中，已知点
在圆
内，动直线
过点
且交圆
于
两点，若△ABC的面积的最大值为
，则实数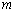
的取值范围为 ．
，若函数
的图象恒在
轴上方，求实数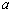
的取值范围．
为正数，且
，则下列各式中正确的一个是 （ ）
B.
C. 
D.
，已知
和
为
的极值点.
和
的值；
，试比较
的大小.
,点E是CD的中点．
面PBD：