题目内容
 记者在街上随机统计10位行人在2014年1月份内接收到的垃圾短信的条数,将数据整理如图所示的茎叶图:
记者在街上随机统计10位行人在2014年1月份内接收到的垃圾短信的条数,将数据整理如图所示的茎叶图:(Ⅰ)计算这组数据的平均数及方差;
(Ⅱ)从这10人中随机抽取2人,记这2人中在这个月内接收到的垃圾短信少于10条的人数为X,求随机变量X的分布列和期望.
考点:离散型随机变量的期望与方差
专题:概率与统计
分析:(Ⅰ)根据公式求样本的平均数与方差;
(Ⅱ)由题意随机变量X=0,1,2,分别求出相应的概率,由此能求出随机变量X的分布列和期望.
(Ⅱ)由题意随机变量X=0,1,2,分别求出相应的概率,由此能求出随机变量X的分布列和期望.
解答:
解:(Ⅰ)
=
(8+9+10+12+13+17+20+20+21+30)=16.
S2=
[(8-16)2+(9-16)2+(10-16)2+(12-16)2+(13-16)2+(17-16)2+(20-16)2+(20-16)2+(21-16)2+(30-16)2]=42.8.
∴这组数据的平均数为16,方差为42.8.
(2)由题意,随机变量X=0,1,2;
P(X=0)=
=
,
P(x=1)=
=
,
P(X=2)=
=
.
随机变量X的分布列为
EX=0×
+1×
+2×
=
.
. |
| x |
| 1 |
| 10 |
S2=
| 1 |
| 10 |
∴这组数据的平均数为16,方差为42.8.
(2)由题意,随机变量X=0,1,2;
P(X=0)=
| ||
|
| 28 |
| 45 |
P(x=1)=
| ||||
|
| 16 |
| 45 |
P(X=2)=
| ||
|
| 1 |
| 45 |
随机变量X的分布列为
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 28 |
| 45 |
| 16 |
| 45 |
| 1 |
| 45 |
| 2 |
| 5 |
点评:本题考查了利用茎叶图求平均数与方差以及随机变量的分布列的问题,解题时要认真审题,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
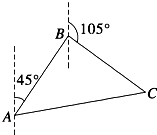 如图所示,我艇在A处发现一走私船在方位角45°且距离为12海里的B处正以每小时10海里的速度向方位角105°的方向逃窜,我艇立即以14海里/小时的速度追击,求我艇追上走私船所需要的最短时间.
如图所示,我艇在A处发现一走私船在方位角45°且距离为12海里的B处正以每小时10海里的速度向方位角105°的方向逃窜,我艇立即以14海里/小时的速度追击,求我艇追上走私船所需要的最短时间.