题目内容
12.函数f(x)=lg(ax3-x2+5a)在(1,2)上递减,则实数a的取值范围是( )| A. | [$\frac{4}{13}$,$\frac{1}{3}$] | B. | ($\frac{4}{13}$,$\frac{1}{3}$] | C. | (-∞,$\frac{1}{3}$] | D. | [$\frac{1}{3}$,+∞) |
分析 令y=ax3-x2+5a,由条件利用复合函数的单调性可得在(1,2)上,y>0且y单调递减,故y′=3ax2-2x<0,再利用二次函数的性质求得a的范围.
解答 解:令y=ax3-x2+5a,则f(x)=lgy,∴在(1,2)上,y>0且y单调递减,
故y′=3ax2-2x=x(3ax-2)<0,∴$\left\{\begin{array}{l}{\frac{2}{3a}>0}\\{8a-4+5a≥0}\\{2≤\frac{2}{3a}}\end{array}\right.$ ①,或 $\left\{\begin{array}{l}{\frac{2}{3a}<0}\\{8a-4+5a>0}\end{array}\right.$ ②.
解①可得$\frac{4}{13}$≤a≤$\frac{1}{3}$,解②求得a无解.
综上可得,$\frac{4}{13}$≤a≤$\frac{1}{3}$,
故选:A.
点评 本题主要考查复合函数的单调性,函数的单调性与导数的关系,填了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.执行如图所示的程序框图,则输出的k值为( )
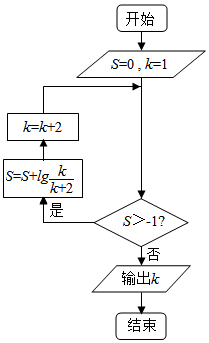

| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
3.设α,β是两个不同的平面,m,n是两条不同的直线,且m?α,n?β( )
| A. | 若m,n是异面直线,则α与β相交 | B. | 若m∥β,n∥α则α∥β | ||
| C. | 若m⊥n,则α⊥β | D. | 若m⊥β,则α⊥β |
20.直线x+y-1=0与2x+2y+3=0的距离是( )
| A. | $\frac{{5\sqrt{2}}}{4}$ | B. | $\frac{{\sqrt{2}}}{4}$ | C. | $2\sqrt{2}$ | D. | $\sqrt{2}$ |
17.已知数列{an}满足2Sn=4an-1.则数列{$\frac{1}{lo{g}_{2}{a}_{n+3}{lo{g}_{2}{a}_{n+2}$}的前100项和为( )
| A. | $\frac{97}{100}$ | B. | $\frac{98}{99}$ | C. | $\frac{99}{100}$ | D. | $\frac{100}{101}$ |
4.已知变量x,y满足约束条件$\left\{{\begin{array}{l}{x+y-1≤0}\\{x-y-1≤0}\\{x-a≥0}\end{array}}\right.$,若$|{\frac{y}{x-2}}|≤\frac{1}{2}$,则实数a的取值范围是( )
| A. | (0,1] | B. | [0,1) | C. | [0,1] | D. | (0,1) |
1.设全集U=R,A={x|0.3x<1},B={x|x<x2-2},则A∩(∁UB)=( )
| A. | {x|-1<x<0} | B. | {x|0<x≤2} | C. | {x|0<x<2} | D. | {x|0<x≤1} |