题目内容
13.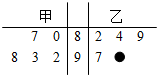 下面茎叶图是甲、乙两人在5次综合测评中成绩(所有成绩取整数)的茎叶图,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为$\frac{4}{5}$.
下面茎叶图是甲、乙两人在5次综合测评中成绩(所有成绩取整数)的茎叶图,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为$\frac{4}{5}$.
分析 由茎叶图,求出甲乙两人的平均成绩,然后利用乙的平均成绩不小于甲的平均成绩的概率,即可得到答案.
解答 解:由茎叶图得,
甲5次综合测评中的成绩分别为87,80,92,93,98,
则甲的平均成绩为:$\frac{1}{5}$(87+80+92+93+98)=90;
设污损数字为x,
则乙5次综合测评中的成绩分别为82,84,89,97,90+x
则乙的平均成绩:$\frac{1}{5}$(82+84+89+97+90+x)=88.4+$\frac{x}{5}$,
当x=9,甲的平均数<乙的平均数,即乙的平均成绩超过甲的平均成绩的概率为$\frac{1}{10}$,
当x=8,甲的平均数=乙的平均数,即乙的平均成绩不小于均甲的平均成绩的概率为$\frac{1}{10}$,
甲的平均成绩超过乙的平均成绩的概率为1-$\frac{1}{10}$-$\frac{1}{10}$=$\frac{4}{5}$.
故答案为:$\frac{4}{5}$.
点评 本题考查了平均数,茎叶图,古典概型概率计算公式的应用问题,是基础题目.

练习册系列答案
相关题目
3.4个男生与3个女生站成一排,如果两端不站女生且3个女生必须相邻的排法有( )
| A. | 144种 | B. | 288种 | C. | 432种 | D. | 576种 |
4.“a=2”是“函数f(x)=x2+3ax-2在区间(-∞,-2]内单调递减”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |
8.在等差数列{an}中,若a1+a2+a3=32,a11+a12+a13=118,则a4+a10=( )
| A. | 45 | B. | 50 | C. | 75 | D. | 60 |
5.已知$A=\{x|y=\sqrt{{2^x}-1}\},B=\{y|y={x^2}+lga\}$,则A?B的充要条件是( )
| A. | ($\frac{1}{10}$,+∞) | B. | 0<a<$\frac{1}{10}$ | C. | 0<a≤1 | D. | a>l |
3.函数f(x)=asinx-bcosx,若f($\frac{π}{4}$+x)=-f($\frac{π}{4}$-x),则函数y=f($\frac{3π}{4}$-2x)的一条对称轴方程是( )
| A. | x=$\frac{π}{6}$ | B. | x=$\frac{π}{4}$ | C. | x=-$\frac{3π}{2}$ | D. | x=-$\frac{2π}{3}$ |