题目内容
3.函数f(x)=asinx-bcosx,若f($\frac{π}{4}$+x)=-f($\frac{π}{4}$-x),则函数y=f($\frac{3π}{4}$-2x)的一条对称轴方程是( )| A. | x=$\frac{π}{6}$ | B. | x=$\frac{π}{4}$ | C. | x=-$\frac{3π}{2}$ | D. | x=-$\frac{2π}{3}$ |
分析 由题意,f($\frac{π}{4}$)=0,求得a=b,故f(x)=$\frac{\sqrt{2}}{2}$asin(x-$\frac{π}{4}$).化简函数y=f($\frac{3π}{4}$-2x)=$\frac{\sqrt{2}}{2}$acos2x,可得它的图象的一条对称轴方程.
解答 解:函数f(x)=asinx-bcosx,若f($\frac{π}{4}$+x)=-f($\frac{π}{4}$-x),则f(x)的图象关于点($\frac{π}{4}$,0)对称,
即 f($\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$a-$\frac{\sqrt{2}}{2}$b=0,故 a=b,故f(x)=a(sinx-cosx)=$\frac{\sqrt{2}}{2}$asin(x-$\frac{π}{4}$).
则函数y=f($\frac{3π}{4}$-2x)=$\frac{\sqrt{2}}{2}$asin($\frac{3π}{4}$-2x-$\frac{π}{4}$)=$\frac{\sqrt{2}}{2}$asin($\frac{π}{2}$-2x )═$\frac{\sqrt{2}}{2}$acos2x 的一条对称轴方程是x=-$\frac{3π}{2}$,
故选:C.
点评 本题主要考查两角和差的三角公式,三角函数的图象的对称性,诱导公式,余弦函数的图象的对称轴,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.己知α∈(0,$\frac{π}{2}$),cos($α+\frac{π}{4}$)=-$\frac{3}{5}$,则tanα=( )
| A. | $\frac{1}{7}$ | B. | 7 | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
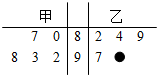 下面茎叶图是甲、乙两人在5次综合测评中成绩(所有成绩取整数)的茎叶图,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为$\frac{4}{5}$.
下面茎叶图是甲、乙两人在5次综合测评中成绩(所有成绩取整数)的茎叶图,其中一个数字被污损,则甲的平均成绩超过乙的平均成绩的概率为$\frac{4}{5}$.