题目内容
3．4个男生与3个女生站成一排，如果两端不站女生且3个女生必须相邻的排法有（ ）| A． | 144种 | B． | 288种 | C． | 432种 | D． | 576种 |
分析 3个女生必须相邻，用捆绑法，作为一个整体，两端不站女生，有3个位置选择，其余男生全排，即可得出结论．
解答 解：3个女生必须相邻，用捆绑法，作为一个整体，两端不站女生，有3个位置选择，其余男生全排，
有${C}_{3}^{1}{A}_{3}^{3}{A}_{4}^{4}$=432种，
故选：C．
点评 本题考查计数原理的应用，考查捆绑法，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
14．下列各组函数f（x）与g（x）的图象相同的是（ ）
| A． | f（x）=$\frac{{{x^2}-4}}{x-2}$，g（x）=x+2 | B． | f（x）=$\sqrt{x^2}，g（x）={（{\sqrt{x}}）^2}$ | ||
| C． | f（x）=$\sqrt{x+1}•\sqrt{x-1}，g（x）=\sqrt{{x^2}-1}$ | D． | f（x）=|x|，g（x）=$\left\{\begin{array}{l}x（x≥0）\\-x（x＜0）\end{array}$ |
11．已知角α的终边上一点坐标为（sin$\frac{5π}{6}$，cos$\frac{5π}{6}$），则角α的最小正值为（ ）
| A． | $\frac{5π}{6}$ | B． | $\frac{11π}{6}$ | C． | $\frac{5π}{3}$ | D． | $\frac{2π}{3}$ |
18．已知复数z1=1-i，z1z2=1+i，则z2=（ ）
| A． | i | B． | -i | C． | 1+i | D． | 1-i |
8．已知x为第三象限角，化简$\sqrt{1-cos2x}$=（ ）
| A． | $\sqrt{2}sinx$ | B． | $\sqrt{2}cosx$ | C． | $-\sqrt{2}sinx$ | D． | $-\sqrt{2}cosx$ |
12．下列命题中，正确的是（ ）
| A． | 若a＞b，c＞d，则ac＞bd | B． | 若ac＞bc，则a＞b | ||
| C． | 若ac2＜bc2，则a＜b | D． | 若a＞b，c＞d，则a-c＞b-d |
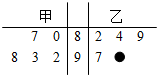下面茎叶图是甲、乙两人在5次综合测评中成绩（所有成绩取整数）的茎叶图，其中一个数字被污损，则甲的平均成绩超过乙的平均成绩的概率为$\frac{4}{5}$．