题目内容
1．求下列函数的值域：（1）y=$\frac{1}{{x}^{2}+2x-3}$；
（2）f（x）=$\frac{{x}^{2}+1}{3x+4}$．
分析 （1）配方得到x2+2x-3=（x+1）2-4≥-4，从而得到-4≤x2+2x-3＜0，或x2+2x-3＞0，从而可以得出$\frac{1}{{x}^{2}+2x-3}$的范围，即得出该函数的值域；
（2）可设y=f（x），从而得到x2-3yx+1-4y=0，看成关于x的一元二次方程，方程有解，从而有△≥0，这样即可得出该函数的值域．
解答 解：（1）x2+2x-3=（x+1）2-4；
∴-4≤x2+2x-3＜0，或x2+2x-3＞0；
∴$\frac{1}{{x}^{2}+2x-3}≤-\frac{1}{4}$，或$\frac{1}{{x}^{2}+2x-3}＞0$；
∴该函数的值域为（-∞，$-\frac{1}{4}$]∪（0，+∞）；
（2）设y=f（x），则3yx+4y=x2+1；
整理得：x2-3yx+1-4y=0，看成关于x的一元二次方程，方程有解；
∴△=9y2-4（1-4y）≥0；
解得y≤-2，或y$≥\frac{2}{9}$；
∴原函数的值域为（-∞，-2]∪[$\frac{2}{9}$，+∞）．
点评 考查函数值域的概念，配方求二次函数值域的方法，以及根据不等式的性质求值域，一元二次方程有解时判别式△的取值情况．
练习册系列答案
相关题目
11．已知角α的终边上一点坐标为（sin$\frac{5π}{6}$，cos$\frac{5π}{6}$），则角α的最小正值为（ ）
| A． | $\frac{5π}{6}$ | B． | $\frac{11π}{6}$ | C． | $\frac{5π}{3}$ | D． | $\frac{2π}{3}$ |
12．下列命题中，正确的是（ ）
| A． | 若a＞b，c＞d，则ac＞bd | B． | 若ac＞bc，则a＞b | ||
| C． | 若ac2＜bc2，则a＜b | D． | 若a＞b，c＞d，则a-c＞b-d |
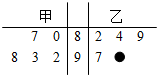下面茎叶图是甲、乙两人在5次综合测评中成绩（所有成绩取整数）的茎叶图，其中一个数字被污损，则甲的平均成绩超过乙的平均成绩的概率为$\frac{4}{5}$．