题目内容
四棱锥![]() ―
―![]() 中,底面
中,底面![]() 为菱形,其对角线
为菱形,其对角线![]() 、
、![]() 交于点
交于点![]() ,
,![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() 中
中![]() ,
,![]()
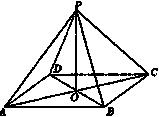
(Ⅰ)求证:![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() ―
―![]() ―
―![]() 的大小。
的大小。
解:(Ⅰ)![]() 为菱形,
为菱形,
![]() 为对角线AC,BD的中点
为对角线AC,BD的中点
![]() 为等边三角形,
为等边三角形,![]() 为等腰三角形,
为等腰三角形,
∴PO⊥AC,PO⊥BD
![]() 平面
平面![]()
(Ⅱ)解法1:由(Ⅰ)知![]() 平面
平面![]() ,作
,作![]() ,垂足为E ,连结
,垂足为E ,连结![]() ,
,
由三垂线定理知,![]() 是二面角C―PA―B的平面角
是二面角C―PA―B的平面角
设![]() 为等边三角形,
为等边三角形,![]()
![]() 为等腰直角三角形,
为等腰直角三角形,![]()
在![]() 中,
中,![]()
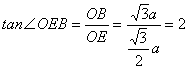
![]() 二面角C―PA―B的大小为
二面角C―PA―B的大小为![]()
解法2(面积射影):由解法一知,![]()
取PB中点F,则![]()
可得![]()
设二面角C―PA―B的大小为![]()
由面积射影定理知,![]()
∴二面角C―PA―B的大小为![]()
解法三向量方法:以O为原点,OA、OB、OP所在直线x、y、z轴,建立空间直角坐标系
则O(0,0,0),A(a,0,0),B(0,![]() a,0),P(0,0,
a,0),P(0,0,![]() a),
a),
![]()
设平面PAB的一个法向量为n=(x,y,z),则![]() ,
,
由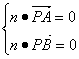 ,得
,得 取z=1,得
取z=1,得![]() )
)
又平面PAC的一个法向量为![]()
cos<n,
∴二面角C―PA―B的大小为![]() .
.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
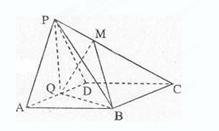

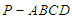 中,底面
中,底面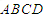 为菱形,
为菱形, ,
, 为
为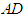 的中点。
的中点。
 ,求证:平面
,求证:平面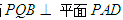 ;
; 在线段
在线段 上,
上,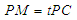 ,试确定
,试确定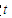 的值,使
的值,使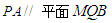 ;
;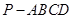 中,底面
中,底面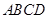 为菱形,
为菱形, ,
, 为
为 的中点。
的中点。 ,求证:平面
,求证:平面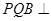 平面
平面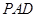 ;
; 在线段
在线段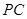 上,
上,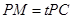 ,试确定
,试确定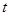 的值,使
的值,使 平面
平面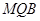 ;
;
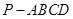 中,底面
中,底面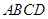 为菱形,
为菱形,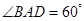 ,
, 为
为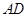 的中点。
的中点。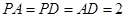
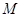 在线段
在线段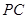 上,
上,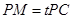 ,试确定
,试确定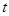 的值,使
的值,使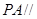 平面
平面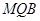 ;
;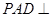 平面ABCD,求二面角
平面ABCD,求二面角 的大小。
的大小。