题目内容
根据下列条件,求圆的方程:
(1)经过P(-2,4)、Q(3,-1)两点,并且在x轴上截得的弦长等于6;
(2)圆心在直线y=-4x上,且与直线l:x+y-1=0相切于点P(3,-2).
解:(1)设圆的方程为x2+y2+Dx+Ey+F=0(D2+ E2-4F>0),
E2-4F>0),
将P、Q两点的坐标分别代入得

又令y=0,得x2+Dx+F=0. ③
设x1,x2是方程③的两根,
由|x1-x2|=6有D2-4F=36, ④
由①、②、④解得
故所求圆的方程为x2+y2-2x-4y-8 =0,或x2+y2-6x-8y=0.
=0,或x2+y2-6x-8y=0.
(2)设所求方程为(x-x0)2+(y-y0)2=r2,
根据已知条件得
 因此所求圆的方程为(x-1)2+(y+4)2=8.
因此所求圆的方程为(x-1)2+(y+4)2=8.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
 .
.
 D.
D.
 2=1
2=1 2+(y-1)2=1
2+(y-1)2=1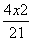 -
-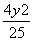 =1 B.
=1 B.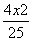 -
-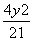 =1 D.
=1 D.