题目内容
14.如图,△O'A'B'是水平放置的△OAB的直观图,则△OAB的周长为( )
| A. | $10+2\sqrt{13}$ | B. | 3$\sqrt{2}$ | C. | $10+4\sqrt{13}$ | D. | 12 |
分析 根据斜二侧画法得到三角形OAB的底面边长0B=4,高OA=2O'A'=6,然后求三角形的周长即可.
解答 解:根据斜二侧画法得到三角形OAB为直角三角形,底面边长0B=4,高OA=2O'A'=6,AB=2$\sqrt{13}$,
∴直角三角形OAB的周长为10+2$\sqrt{13}$.
故选:A.
点评 本题主要考查平面图形的直观图的应用,要求熟练掌握斜二测画法的边长关系,比较基础.

练习册系列答案
相关题目
4.阅读如图所示的程序框图,则输出的S的值是( )


| A. | $\frac{8}{9}$ | B. | $\frac{9}{10}$ | C. | $\frac{7}{8}$ | D. | $\frac{6}{7}$ |
2.已知tanα=-$\frac{3}{4}$,且α是第二象限角,则cosα的值为( )
| A. | $\frac{3}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $-\frac{4}{5}$ |
3.偶函数f(x)在(0,+∞)上递增,a=f(log2$\frac{1}{3}$)b=f($\frac{3}{2}$)c=f(log32),则下列关系式中正确的是( )
| A. | <b<c | B. | a<c<b | C. | c<a<b | D. | c<b<a |
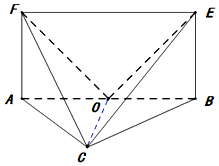 如图,四边形ABEF为矩形,AC=BC,AB=2AF=FC=2,$OC=\sqrt{2}$.O为AB的中点.
如图,四边形ABEF为矩形,AC=BC,AB=2AF=FC=2,$OC=\sqrt{2}$.O为AB的中点.