题目内容
已知圆 ,是否存在斜率为
,是否存在斜率为 的直线
的直线 ,使以
,使以 被圆截得的弦
被圆截得的弦 为直径的圆过原点?若存在,求出直线
为直径的圆过原点?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
解析:法1.假设存在斜率为 的直线
的直线 ,满足题意,则OA⊥OB.
,满足题意,则OA⊥OB.
设直线 的方程是
的方程是 ,其与圆
,其与圆 的交点
的交点 ,
, 的坐标分别为
的坐标分别为 ,
,
则 ,[ 即
,[ 即 . ①
. ①
由 消去
消去 得,
得, ,
,
∴ ,
, , ②
, ②

 . ③
. ③
把②③式代入①式,得 ,解得
,解得 或
或 ,
,
而 或
或 都使得
都使得 成立.
成立.
故存在直线 满足题意,其方程为
满足题意,其方程为 或
或
法2. 圆C化成标准方程为 , 半径
, 半径
假设存在以 为直径的圆的圆心为
为直径的圆的圆心为 ,
,
则直线 的方程是
的方程是 ,即
,即 ,则
,则
 ,
, ,即
,即 ①
①
且  ,
,
∵以 为直径的圆
为直径的圆 过原点,∴
过原点,∴ ,
,
所以 ②
②
把①代入②得, ,∴
,∴ 或
或 ,
,
当 或
或 时,
时, ,此时直线的方程为
,此时直线的方程为 ;
;
当 时,
时, ,此时直线
,此时直线 的方程为
的方程为 ;
;
故这样的直线 是存在的,方程为
是存在的,方程为 或
或

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案
相关题目
 与连接
与连接 、
、 的线段相交,求
的线段相交,求 的取值范围.
的取值范围. 经过
经过 两点,圆心在
两点,圆心在 轴上,则圆
轴上,则圆 B.
B. C.
C. D.
D.
 向圆
向圆 所引的切线方程.
所引的切线方程. 与圆
与圆 相交于
相交于 、
、 两点,则
两点,则 的值为( )
的值为( ) D.与
D.与 有关的数值
有关的数值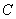 :
: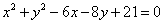 和直线
和直线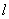 :
: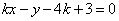 .
.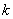 取何值时直线
取何值时直线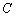 总相交;
总相交; 上到直线
上到直线 的距离为
的距离为 的点的个数是 .
的点的个数是 .