题目内容
已知圆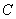
：
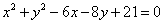和直线
：
．
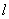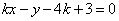（1）证明：不论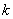
取何值时直线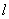和圆
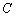总相交；
（2）当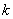取何值时，圆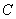被直线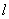截得的弦长最短？并求最短的弦的长度．
【解析】（1）圆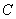的方程可化为：
， 圆心为
，半径
．
直线
的方程可化为：
，∴直线过定点
．
∵定点到圆心的距离
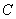， ∴定点 在圆内部，
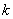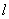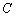∴不论取何值，直线和圆总相交．
（2）当直线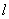与
垂直时，圆被直线截得的弦最短．
∵过
两点的直线的斜率
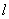， 故直线的斜率
，
最短弦长
练习册系列答案
相关题目
作直线
分别交
、
轴的正半轴于
、
两点．当
取最小值时，求直线
与圆
的位置关系是（ ）
，是否存在斜率为
的直线
，使以
为直径的圆过原点？若存在，求出直线
关于点
对称的圆
的方程为 
，斜率为1直线
与圆
相交于
、
两点，
为坐标原点， 
，求出直线