题目内容
(本题满分12分)
如图, 是⊙
是⊙ 的直径,
的直径, 垂直于⊙
垂直于⊙ 所在的平面,
所在的平面, 是圆周上不同于
是圆周上不同于 的一动点.
的一动点.
(1)证明:面PAC 面PBC;
面PBC;
(2)若 ,则当直线
,则当直线 与平面
与平面 所成角正切值为
所成角正切值为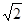 时,求直线
时,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(1) 证明见解析;(2) 与平面
与平面 所成角正弦值为
所成角正弦值为 。
。
解析试题分析:(1) 证明略 ----------------6分
(2)如图,过 作
作 ,
, ,
,
 ,则
,则 即是要求的角。…..8分
即是要求的角。…..8分

 即是
即是 与平面
与平面 所成角,…..9分
所成角,…..9分 ,又
,又

 …..10分
…..10分 在
在 中,
中, ,…..11分
,…..11分
在 中,
中, ,即
,即 与平面
与平面 所成角正弦值为
所成角正弦值为 。..12分
。..12分
考点:本题主要考查立体几何中线面垂直、直线与平面所成的角。
点评:典型题,立体几何中线面关系与线线关系的相互转化是高考重点考查内容,角的计算问题,要注意“一作、二证、三计算”。

练习册系列答案
相关题目
 与圆
与圆 交于
交于 、
、 两点,记△
两点,记△ 的面积为
的面积为 (其中
(其中 为坐标原点).
为坐标原点). ,
,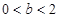 时,求
时,求 ,
, 时,求实数
时,求实数 的值.
的值. ,过原点
,过原点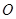 的直线
的直线 与圆
与圆 相交于
相交于 两点
两点 的长为
的长为 ,求直线
,求直线 为定值。
为定值。 .
. 是(1)中曲线C上的动点,求
是(1)中曲线C上的动点,求 的取值范围.
的取值范围. |PD|.
|PD|.
 上,与
上,与 轴相切,且被直线
轴相切,且被直线 截得弦长为
截得弦长为 的圆的方程.
的圆的方程.  的圆形村落,
的圆形村落, 、
、 两人同时从村落中心出发。
两人同时从村落中心出发。 ,且后来
,且后来
 的顶点
的顶点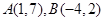 ,重心
,重心
 相交,所得公共弦平行于已知直线
相交,所得公共弦平行于已知直线 ,又圆C经过点A(-2,3),B(1,4),求圆C的方程。
,又圆C经过点A(-2,3),B(1,4),求圆C的方程。