题目内容
13.已知f(x)=$\left\{\begin{array}{l}{1-x-2{x}^{2}}&{x≤0}\\{|lgx|}&{x>0}\end{array}\right.$若关于x的方程f(x)=a有四个实根x1,x2,x3,x4,则这四根之积x1,x2,x3,x4的取值范围是( )| A. | [0,$\frac{1}{2}$) | B. | [0,$\frac{1}{4}$) | C. | [0,$\frac{1}{8}$) | D. | [0,$\frac{1}{16}$) |
分析 确定x3x4=1,x1x2x3x4=x1x2,利用关于x的方程f(x)=a有四个实根x1,x2,x3,x4,可得1≤a<$\frac{9}{8}$,由1-x-2x2=a可得x1x2=$\frac{a-1}{2}$∈[0,$\frac{1}{16}$),即可得出结论.
解答 解:由题意,-lgx3=lgx4,∴x3x4=1,
∴x1x2x3x4=x1x2,
y=1-x-2x2的顶点坐标为(1,$\frac{9}{8}$),x=0时,y=1
∵关于x的方程f(x)=a有四个实根x1,x2,x3,x4,
∴1≤a<$\frac{9}{8}$
由1-x-2x2=a可得x1x2=$\frac{a-1}{2}$∈[0,$\frac{1}{16}$),
∴四根之积x1,x2,x3,x4的取值范围是[0,$\frac{1}{16}$),
故选:D.
点评 本题考查分段函数,考查韦达定理的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
3.函数y=|x|-2cosx的图象大致是( )
| A. | 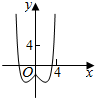 | B. | 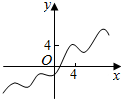 | C. | 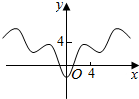 | D. | 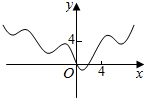 |
8.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$(a>0,b>0)的左、右焦点分别为F1、F2,点M是双曲线右支上一点,且MF1⊥MF2,延长MF2交双曲线C于点P,若|MF1|=|PF2|,则双曲线C的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{\sqrt{10}}{2}$ | D. | $\sqrt{6}$ |
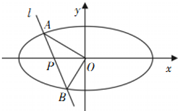 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,短轴一个端点到右焦点的距离为2,直线l过点P(-1,0)且与曲线C交于A,B两点.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,短轴一个端点到右焦点的距离为2,直线l过点P(-1,0)且与曲线C交于A,B两点.