题目内容
4.如图,P∉平面ABC,PA=PB=PC,∠APB=∠APC=60°,∠BPC=90°,求证:平面ABC⊥平面PBC.
分析 要证明面面垂直,只要在其平面内找一条线,然后证明直线与另一平面垂直即可.显然BC中点D,证明AD垂直平PBC即可.
解答 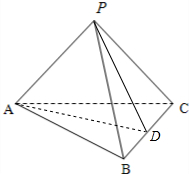 证明:取BC中点D 连结AD、PD
证明:取BC中点D 连结AD、PD
∵PA=PB;∠APB=60°
∴△PAB为正三角形
同理△PAC为正三角形
设PA=a
在Rt△BPC中,PB=PC=a,BC=$\sqrt{2}$a
∴PD=$\frac{\sqrt{2}}{2}$a
在△ABC中,AD=$\frac{\sqrt{2}}{2}$a
∵AD2+PD2=($\frac{\sqrt{2}}{2}$a)2+($\frac{\sqrt{2}}{2}$a)2=a2=AP2
∴△APD为直角三角形
即AD⊥DP
又∵AD⊥BC
∴AD⊥平面PBC
∴平面ABC⊥平面PBC.
点评 本题考查直线与平面、平面与平面垂直的判定,考查学生分析解决问题的能力,证明AD⊥DP是关键.

练习册系列答案
相关题目
13.已知f(x)=$\left\{\begin{array}{l}{1-x-2{x}^{2}}&{x≤0}\\{|lgx|}&{x>0}\end{array}\right.$若关于x的方程f(x)=a有四个实根x1,x2,x3,x4,则这四根之积x1,x2,x3,x4的取值范围是( )
| A. | [0,$\frac{1}{2}$) | B. | [0,$\frac{1}{4}$) | C. | [0,$\frac{1}{8}$) | D. | [0,$\frac{1}{16}$) |
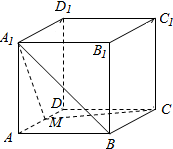 如图,在长方体ABCD-A1B1C1D1中,已知AB=AA1=a,BC=$\sqrt{2}$a,M是AD的中点.
如图,在长方体ABCD-A1B1C1D1中,已知AB=AA1=a,BC=$\sqrt{2}$a,M是AD的中点.