题目内容
3.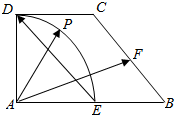 在直角梯形ABCD中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E、F分别为AB、BC的中点.点P在以A为圆心,AD为半径的圆弧$\widehat{DE}$上运动(如图所示),若 $\overrightarrow{AP}$=λ $\overrightarrow{ED}$+μ $\overrightarrow{AF}$,其中λ,μ∈R.则$\frac{2λ}{μ}$的取值范围是[-1,3].
在直角梯形ABCD中,AB⊥AD,DC∥AB,AD=DC=1,AB=2,E、F分别为AB、BC的中点.点P在以A为圆心,AD为半径的圆弧$\widehat{DE}$上运动(如图所示),若 $\overrightarrow{AP}$=λ $\overrightarrow{ED}$+μ $\overrightarrow{AF}$,其中λ,μ∈R.则$\frac{2λ}{μ}$的取值范围是[-1,3].
分析 建立如图所示的坐标系,则A(0,0),E(1,0),D(0,1),F(1.5,0.5),P(cosα,sinα)(0°≤α≤90°),λ,μ用参数进行表示,再利用函数的单调性即可求出范围
解答 解:建立如图所示的坐标系,则A(0,0),E(1,0),D(0,1),F(1.5,0.5),P(cosα,sinα)(0°≤α≤90°),
∵$\overrightarrow{AP}$=λ $\overrightarrow{ED}$+μ $\overrightarrow{AF}$,
∴(cosα,sinα)=λ(-1,1)+μ(1.5,0.5),
∴cosα=-λ+1.5μ,sinα=λ+0.5μ,
∴λ=$\frac{1}{4}$(3sinα-cosα),μ=$\frac{1}{2}$(cosα+sinα),
∴$\frac{2λ}{μ}$=$\frac{3sinα-cosα}{cosα+sinα}$=$\frac{3tanα-1}{tanα+1}$=3-$\frac{4}{1+tanα}$,
设f(α)=3-$\frac{4}{1+tanα}$,易知函数f(α)为增函数,
∵0≤α≤90°,
∴f(0)≤f(α)≤f(90°)
∴-1≤f(α)≤3
∴$\frac{2λ}{μ}$的取值范围是[-1,3].
故答案为:[-1,3].
点评 本题考查平面向量知识的运用,考查学生的计算能力,正确利用坐标系是关键,属于中档题

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.设等差数列{an}的前n项和为Sn,若a1=-11,a4+a6=-6,则a3等于( )
| A. | 16 | B. | 37 | C. | -7 | D. | 9 |
19.函数f(x)=2x+log2|x|的零点个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |