题目内容
5.已知数列{an}的前n项和为Sn,且对任意正整数n,都有${a_n}=\frac{3}{4}{S_n}+2$成立.(1)记bn=log2an,求数列{bn}的通项公式;
(2)设${c_n}=\frac{1}{{{b_n}{b_{n+1}}}}$,求证:数列{cn}的前n项和Tn<$\frac{1}{6}$.
分析 (1)根据数列的递推公式即可求出数列{an}为等比数列,根据对数的运算性质可得bn=2n+1,
(2)根据裂项求和和放缩法即可得到答案.
解答 解:(1)在${a_n}=\frac{3}{4}{S_n}+2$中令n=1得a1=8,
因为对任意正整数n,都有${a_n}=\frac{3}{4}{S_n}+2$成立,所以an+1=$\frac{3}{4}$Sn+1+2,
两式相减得an+1-an=$\frac{3}{4}$an+1,
所以an+1=4an,
又a1≠0,
所以数列{an}为等比数列,
所以an=8•4n-1=22n+1,
所以bn=log2an=2n+1,
(2)${c_n}=\frac{1}{{({2n+1})({2n+3})}}=\frac{1}{2}({\frac{1}{2n+1}-\frac{1}{2n+3}})$,
所以${T_n}=\frac{1}{2}[{({\frac{1}{3}-\frac{1}{5}})+({\frac{1}{5}-\frac{1}{7}})+…+({\frac{1}{2n+1}-\frac{1}{2n+3}})}]=\frac{1}{2}({\frac{1}{3}-\frac{1}{2n+3}})=\frac{n}{{3({2n+3})}}$<$\frac{1}{6}$.
点评 本题考查了根据数列的递推公式求通项公式和裂项求和以及放缩法,属于中档题.

练习册系列答案
相关题目
15.已知复数z满足($\sqrt{3}$+3i)z=3i,则|z|=( )
| A. | $\sqrt{2}$ | B. | 1 | C. | $\sqrt{3}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
16.?x∈[-2,1],使不等式ax3-x2+4x+3≥0成立,则实数a的取值范围是( )
| A. | [-5,-3] | B. | [-6,-$\frac{9}{8}$] | C. | [-6,-2] | D. | [-4,-3] |
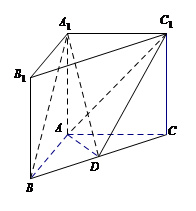 如图,在直三棱柱A1B1C1-ABC中,AB=AC=AA1,$BC=\sqrt{2}AB$,点D是BC的中点.
如图,在直三棱柱A1B1C1-ABC中,AB=AC=AA1,$BC=\sqrt{2}AB$,点D是BC的中点.