题目内容
8.非零向量($\overrightarrow{a}$+3$\overrightarrow{b}$)⊥(2$\overrightarrow{a}$-$\overrightarrow{b}$),($\overrightarrow{a}$-2$\overrightarrow{b}$)⊥(2$\overrightarrow{a}$+$\overrightarrow{b}$),求向量$\overrightarrow{a}$与$\overrightarrow{b}$夹角的余弦值.分析 运用向量垂直的条件:数量积为0,可得2$\overrightarrow{a}$2+5$\overrightarrow{a}$•$\overrightarrow{b}$-3$\overrightarrow{b}$2=0,①,2$\overrightarrow{a}$2-3$\overrightarrow{a}$•$\overrightarrow{b}$-2$\overrightarrow{b}$2=0,②,再求向量$\overrightarrow{a}$,$\overrightarrow{b}$的模,再由向量的夹角公式,计算即可得到所求值.
解答 解:($\overrightarrow{a}$+3$\overrightarrow{b}$)⊥(2$\overrightarrow{a}$-$\overrightarrow{b}$),可得
($\overrightarrow{a}$+3$\overrightarrow{b}$)•(2$\overrightarrow{a}$-$\overrightarrow{b}$)=0,
即为2$\overrightarrow{a}$2+5$\overrightarrow{a}$•$\overrightarrow{b}$-3$\overrightarrow{b}$2=0,①
($\overrightarrow{a}$-2$\overrightarrow{b}$)⊥(2$\overrightarrow{a}$+$\overrightarrow{b}$),
可得($\overrightarrow{a}$-2$\overrightarrow{b}$)•(2$\overrightarrow{a}$+$\overrightarrow{b}$)=0,
即为2$\overrightarrow{a}$2-3$\overrightarrow{a}$•$\overrightarrow{b}$-2$\overrightarrow{b}$2=0,②
由①②解得,$\overrightarrow{b}$2=8$\overrightarrow{a}$•$\overrightarrow{b}$,
$\overrightarrow{a}$2=$\frac{19}{2}$$\overrightarrow{a}$•$\overrightarrow{b}$,
则cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|•|\overrightarrow{b}|}$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{\sqrt{8\overrightarrow{a}•\overrightarrow{b}•(\frac{19}{2}\overrightarrow{a}•\overrightarrow{b})}}$=$\frac{\sqrt{19}}{38}$.
点评 本题考查向量垂直的条件:数量积为0,向量的平方即为模的平方,考查向量的夹角公式的运用,属于中档题.

 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案| A. | 40 | B. | -80 | C. | 120 | D. | -160 |
| A. | $\frac{1}{3}$ | B. | $\sqrt{3}$ | C. | 3 | D. | 9 |
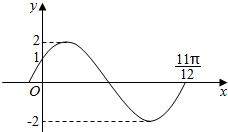 如图所示为函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象.
如图所示为函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象.