题目内容
正四棱锥的侧棱长与底面边长都是1,则侧棱与底面所成的角为( )
| A.75° | B.60° | C.45° | D.30° |
C
解析试题分析:如图,四棱锥P-ABCD中,过P作PO⊥平面ABCD于O,连接AO,则AO是AP在底面ABCD上的射影.∴∠PAO即为所求线面角,
∵AO= ,PA=1,∴cos∠PAO=
,PA=1,∴cos∠PAO= ,.∴∠PAO=45°,即所求线面角为45°.故答案为C.
,.∴∠PAO=45°,即所求线面角为45°.故答案为C.
考点:直线与平面所成的角;棱锥的结构特征.
点评:本题考查棱锥的结构特征,以及求直线和平面成的角的方法,体现了数形结合的数学思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
设l、m是两条不同的直线,a,β是两个不同的平面,有下列命题:
①l//m,m a,则l//a ;② l//a,m//a 则 l//m; ③a丄β,l
a,则l//a ;② l//a,m//a 则 l//m; ③a丄β,l a,则l丄β; ④l丄a,m丄a,则l//m.
a,则l丄β; ④l丄a,m丄a,则l//m.
其中正确的命题的个数是( )
| A.1 | B.2 | C.3 | D.4 |
如图,在长方体 中,
中, ,
, 则
则 与平面
与平面 所成角的正弦值为 ( )
所成角的正弦值为 ( )
A. | B. | C. | D. |
在四边形 中,
中, ∥
∥ ,
, ,将
,将 沿
沿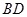 折起,使平面
折起,使平面 平面
平面 ,构成三棱锥
,构成三棱锥 ,则在三棱锥
,则在三棱锥 中,下列命题正确的是( )
中,下列命题正确的是( )
A.平面 平面 平面 | B.平面 平面 平面 |
C.平面 平面 平面 | D.平面 平面 平面 |
如图,长方体ABCD—A1B1C1D1中,BB1=BC,P为C1D1上一点,则异面直线PB与B1C所成角的大小( )
| A.是45° | B.是60° |
| C.是90° | D.随P点的移动而变化 |
设 是直线,
是直线, ,
, 是两个不同的平面,下列命题正确的是( ).
是两个不同的平面,下列命题正确的是( ).
A.若 , , ,则 ,则 | B.若 , , ,则 ,则 |
C.若 , , ,则 ,则 | D.若 , ,  ,则 ,则 |
 的棱
的棱 上的两点,分别在
上的两点,分别在 内作垂直于棱
内作垂直于棱 D.
D.
 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,给出下列条件,能得到
是两个不同的平面,给出下列条件,能得到 的是( )
的是( )



 B.
B.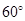 C.
C. D.
D.