题目内容
如图,长方体ABCD—A1B1C1D1中,BB1=BC,P为C1D1上一点,则异面直线PB与B1C所成角的大小( )
| A.是45° | B.是60° |
| C.是90° | D.随P点的移动而变化 |
C
解析试题分析:画出图形,利用长方体的性质,三垂线定理推出BP⊥B1C,得到选项.解:∵D1C1⊥面BCC1B1,
∴BC1为BP在面BCC1B1内的射影,又BC1=B1C,∴BC1⊥B1C,∴BP⊥B1C.异面直线PB与B1C所成角的大小90°.故选C.
考点:长方体的性质
点评:本题主要考查长方体的性质和求异面直线所成角的求法,三垂线定理的应用,考查空间想象能力,计算能力

练习册系列答案
相关题目
平面 外有两条直线
外有两条直线 和
和 ,如果
,如果 和
和 在平面
在平面 内的射影分别是
内的射影分别是 和
和 ,给出下列四个命题:①
,给出下列四个命题:① ②
② ③
③ 与
与 相交
相交
 与
与 相交或重合 ④
相交或重合 ④ 与
与 平行
平行
 与
与 平行或重合,其中不正确的命题的个数是( )
平行或重合,其中不正确的命题的个数是( )
| A.4个 | B.3个 | C.2个 | D. 1 |
已知 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,下列命题中错误的是( )
是三个不同的平面,下列命题中错误的是( )
A.若 ,则 ,则 ∥ ∥ |
B.若 ∥ ∥ , , ∥ ∥ ,则 ,则 ∥ ∥ |
C.若 ∥ ∥ ,则 ,则 ∥ ∥ |
D.若 是异面直线, 是异面直线, ∥ ∥ , , ∥ ∥ ,则 ,则 ∥ ∥ |
正方体的棱长为1, 、
、 、
、 分别为三条棱的中点,
分别为三条棱的中点, 、
、 是顶点,那么点
是顶点,那么点 到截面
到截面 的距离是( )
的距离是( )
A. | B. |
C. | D. |
正四棱锥的侧棱长与底面边长都是1,则侧棱与底面所成的角为( )
| A.75° | B.60° | C.45° | D.30° |
已知直线 及两个平面
及两个平面 、
、 ,下列命题正确的是 ( )
,下列命题正确的是 ( )
A.若 ,则 ,则 | B.若 ,则 ,则 |
C.若 , 则 , 则 | D.若 ,则 ,则 |
关于直线 与平面
与平面 ,有以下四个命题:
,有以下四个命题:
①若 且
且 ,则
,则 ; ②若
; ②若 且
且 ,则
,则 ;
;
③若 且
且 ,则
,则 ; ④若
; ④若 且
且 ,则
,则 ;
;
其中真命题的序号是( )
| A.①② | B.③④ | C.①④ | D.②③ |
已知 是两个不同的平面,
是两个不同的平面, 是不同的直线,下列命题不正确的是
是不同的直线,下列命题不正确的是
A.若 则 则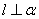 |
B.若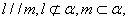 则 则 |
C.若 则 则 |
D.若 ,则 ,则 |
设 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,下列命题中正确的是( )
是两个不同的平面,下列命题中正确的是( )
A.若 , , , , ,则 ,则 |
B.若 , , , , ,则 ,则 |
C.若 , , , , ,则 ,则 |
D.若 , , , , ,则 ,则 |