题目内容
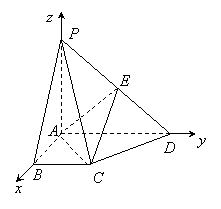
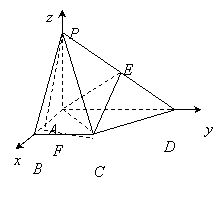
如图,在四棱锥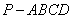 中,
中,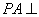 平面
平面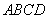 ,底面
,底面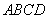 是直角梯形,
是直角梯形,
 ,
,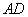 ∥
∥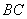 ,且
,且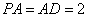 ,
,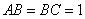 ,
,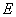 为
为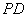 的中点.
的中点.
(Ⅰ)求证: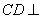 平面
平面 ;
;
(Ⅱ)求二面角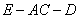 的余弦值;
的余弦值;
(Ⅲ)在线段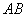 上是否存在一点
上是否存在一点 (不与
(不与 两点重合),使得
两点重合),使得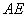 ∥平面
∥平面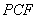 ?若存在,求出
?若存在,求出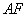 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
 |
(Ⅰ)证明:
因为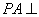 平面
平面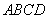 ,
,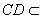 平面
平面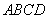 ,
,
所以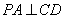 .
.
取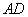 的中点
的中点 ,连结
,连结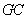 ,
,
因为底面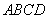 为直角梯形,
为直角梯形,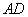 ∥
∥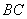 ,
, ,且
,且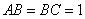 ,
,
所以四边形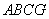 为正方形,所以
为正方形,所以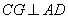 ,且
,且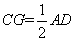 ,
,
所以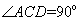 ,即
,即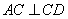 .
.
又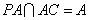 ,所以
,所以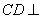 平面
平面 .
.
(Ⅱ)解:如图,以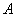 为坐标原点,
为坐标原点,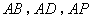 所在直线分别为
所在直线分别为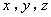 轴建立空间直角坐标系
轴建立空间直角坐标系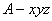 .
.
则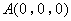 ,
,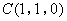 ,
,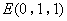 ,
,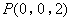 ,
,
所以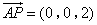 ,
,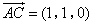 ,
,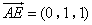 .
.
 因为
因为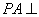 平面
平面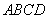 ,所以
,所以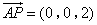 为平面
为平面 的一个法向量.
的一个法向量.
设平面 的法向量为
的法向量为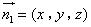 ,
,
由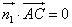 ,
, 得
得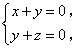
令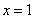 ,则
,则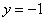 ,
,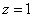 ,
,
所以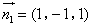 是平面
是平面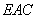 的一个法向量.
的一个法向量.
所以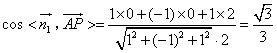
因为二面角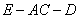 为锐角, 所以二面角
为锐角, 所以二面角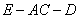 的余弦值为
的余弦值为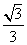 .
.
(Ⅲ)解:假设在线段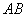 上存在点
上存在点 (不与
(不与 两点重合),使得
两点重合),使得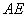 ∥平面
∥平面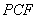 .
.
 设
设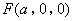 ,则
,则 ,
,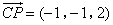 .
.
设平面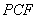 的法向量为
的法向量为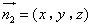 ,
,
由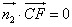 ,
,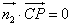 得
得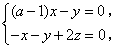
令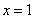 ,则
,则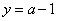 ,
,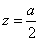 ,
,
所以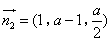 是平面
是平面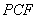 的一个法向量.…12分
的一个法向量.…12分
因为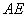 ∥平面
∥平面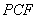 ,所以
,所以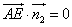 ,即
,即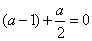 ,
,
解得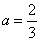 ,
,
所以在线段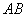 上存在一点
上存在一点 (不与
(不与 两点重合),使得
两点重合),使得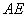 ∥平面
∥平面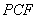 ,且
,且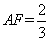 .
.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
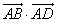 等于
等于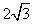 (B)2 (C)
(B)2 (C)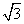 (D)1
(D)1 的值为
的值为 ,
,




 中,
中, ,
, 是
是 为半径的圆与
为半径的圆与 切于点
切于点 ,
, ,
, ,则
,则 的长为 .
的长为 . 
 ,
, ,
, ,则
,则 ( )
( ) (B)
(B) (C)
(C) (D)
(D)
 满足
满足 ,
, ,则公差
,则公差 ______;
______; ______.
______.  的图象,只要将函数
的图象,只要将函数 的图象
的图象 个单位 B.向右平移
个单位 B.向右平移 个单位 D.向右平移
个单位 D.向右平移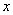 轴的非负半轴为极轴建立极坐标系.已知直线l的参数方程为
轴的非负半轴为极轴建立极坐标系.已知直线l的参数方程为 为参数),圆
为参数),圆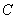 的极坐标方程为
的极坐标方程为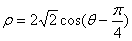 .
.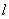 对称,求
对称,求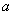 的值;
的值;