题目内容
已知平行四边形ABCD中,AB=1,AD=2,∠DAB=60o,则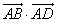 等于
等于
(A)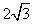 (B)2 (C)
(B)2 (C)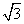 (D)1
(D)1
D

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
题目内容
已知平行四边形ABCD中,AB=1,AD=2,∠DAB=60o,则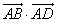 等于
等于
(A)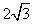 (B)2 (C)
(B)2 (C)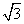 (D)1
(D)1
D

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案