题目内容
工厂生产某种产品，次品率p与日产量x（万件）间的关系为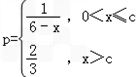
（c为常数，且0＜c＜6），已知每生产1件合格产品盈利3元，每出现1件次品亏损1.5元．
（1）将日盈利额y（万元）表示为日产量x（万件）的函数；
（2）使日盈利额最大，日产量应为多少万件？（注：次品率=
）
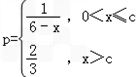（c为常数，且0＜c＜6），已知每生产1件合格产品盈利3元，每出现1件次品亏损1.5元．（1）将日盈利额y（万元）表示为日产量x（万件）的函数；
（2）使日盈利额最大，日产量应为多少万件？（注：次品率=
）解：（1）当x＞c时，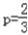
∴ 
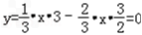
当0＜x≤c时，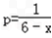
∴
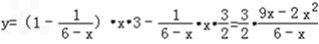
∴日盈利额y（万元）与日产量x（万件）的函数关系式为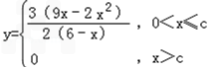
（2）由（1）知，当x＞c时，日盈利额为0．
当0＜x≤c时，∵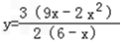
∴ 
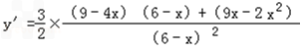
令y'=0得x=3或x=9（舍去）
①当0＜c＜3时， ∵y'＞0，∴y在区间（0，c]]上单调递增，
∴y最大值=f（c）=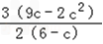
，此时x=c
②当3≤c≤6时，在（0，3）上，y'＞0，在（3，6）上y'＜0
∴y最大值=f（3）=
综上，若0＜c＜3，则当日产量为c万件时，日盈利额最大；
若3≤c＜6，则当日产量为3万件时，日盈利额最大
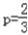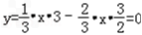
∴ 当0＜x≤c时，
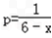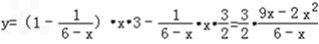
∴ ∴日盈利额y（万元）与日产量x（万件）的函数关系式为
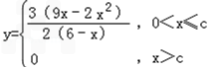
（2）由（1）知，当x＞c时，日盈利额为0．
当0＜x≤c时，∵
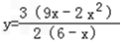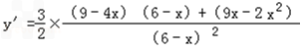
∴ 令y'=0得x=3或x=9（舍去）
①当0＜c＜3时， ∵y'＞0，∴y在区间（0，c]]上单调递增，
∴y最大值=f（c）=
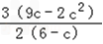，此时x=c②当3≤c≤6时，在（0，3）上，y'＞0，在（3，6）上y'＜0
∴y最大值=f（3）=
综上，若0＜c＜3，则当日产量为c万件时，日盈利额最大；
若3≤c＜6，则当日产量为3万件时，日盈利额最大
练习册系列答案
优质课堂快乐成长系列答案
相关题目
，已知生产一件合格产品能盈利25万元，生产一件次品次亏损10万元，假设该产品任何两件之间合格与否相互没有影响。
与月份
的关系，模拟的函数可以选用二次函数
（
为常数，且
）或函数
（
为常数，且
）。已知4月份该产品的产量为
万件，请问用以上哪个函数作为模拟函数较好，并说明理由。