题目内容
已知函数 ,
, ,
, .
.
(1)若 ,试判断并证明函数
,试判断并证明函数 的单调性;
的单调性;
(2)当 时,求函数
时,求函数 的最大值的表达式
的最大值的表达式 .
.
解:(1)判断:若 ,函数
,函数 在
在 上是增函数. ……… 1分
上是增函数. ……… 1分
证明:当 时,
时, ,
,
在区间 上任意
上任意 ,设
,设 ,
,

所以 ,即
,即 在
在 上是增函数. ………………4分
上是增函数. ………………4分
(注:用导数法证明或其它方法说明也同样给5分) www.zxs
(2)因为 ,所以
,所以 ………………6分
………………6分
①当 时,
时, 在
在 上是增函数,在
上是增函数,在 上也是增函数,
上也是增函数,
所以当 时,
时, 取得最大值为
取得最大值为 ; ……………… 7分
; ……………… 7分
②当 时,
时, 在
在 上是增函数,在
上是增函数,在 上是减函数,
上是减函数,
在 上是增函数, ………………9分
上是增函数, ………………9分
而 ,
,
当 时,
时, ,当
,当 时,函数
时,函数 取最大值为
取最大值为 ;
;
当 时,
时, ,当
,当 时,函数
时,函数 取最大值为
取最大值为 ;
;
………………11分
综上得, ……………… 12分
……………… 12分

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
 是公差不为零的等差数列,
是公差不为零的等差数列, ,且
,且 是
是 的等比中项.
的等比中项. 为数列
为数列 项和,求使
项和,求使 成立的所有
成立的所有 ,
, ,则
,则 _________ .
_________ . ,如果p是q的充分不必要条件,则实数k的取值范围是( )
,如果p是q的充分不必要条件,则实数k的取值范围是( ) B.
B.  C.
C.  D.
D. 
 有零点,则
有零点,则 的取值范围是___________.
的取值范围是___________. 与直线x=1,x=4及x轴所围成的区域的面积是( )
与直线x=1,x=4及x轴所围成的区域的面积是( ) B.ln2 C.2ln2 D.ln2-2
B.ln2 C.2ln2 D.ln2-2 中角
中角 、
、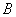 、
、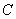 的对边分别是
的对边分别是 、
、 、
、 ,若
,若 ,
, ________.
________.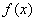 是定义在R上的偶函数,且满足
是定义在R上的偶函数,且满足 ,当
,当 时,
时, ,则
,则 的值为 ( )
的值为 ( )