题目内容
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,PD⊥底面ABCD.
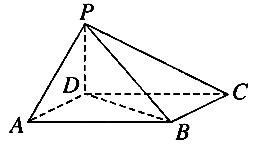
(1)证明:PA⊥BD;
(2)若PD=AD,求二面角A-PB-C的余弦值.
解:(1)证明:因为∠DAB=60°,AB=2AD,
由余弦定理得BD= AD.
AD.
从而BD2+AD2=AB2,故BD⊥AD.
又PD⊥底面ABCD,可得BD⊥PD.
所以BD⊥平面PAD.故PA⊥BD.
 (2)如图,以D为坐标原点,AD的长为单位长,射线DA为x轴的正半轴建立空间直角坐标系D-xyz,则
(2)如图,以D为坐标原点,AD的长为单位长,射线DA为x轴的正半轴建立空间直角坐标系D-xyz,则
A(1,0,0),B (0,
(0, ,0),C(-1,
,0),C(-1, ,0),P(0,0,1).
,0),P(0,0,1).
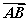 =(-1,
=(-1, ,0),
,0), =(0,
=(0, ,-1),
,-1),
 =(-1,0,0).
=(-1,0,0).


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


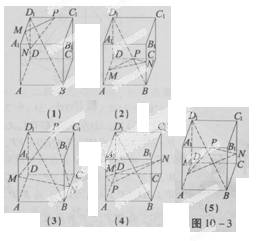
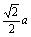 ,D是A1C1的中点。
,D是A1C1的中点。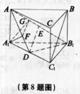
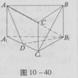
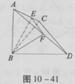
 AB=1,M是PB的中点。
AB=1,M是PB的中点。
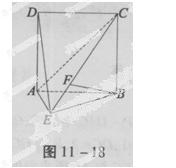
 =
=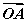 +t
+t 为ξ。
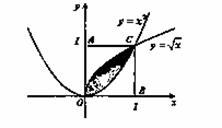
为ξ。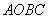 内,曲线
内,曲线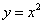 和曲线
和曲线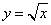 围成一个叶形图(阴影部分),向正方形
围成一个叶形图(阴影部分),向正方形