题目内容
18.设椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,P是C上的点,PF1⊥PF2,∠PF1F2=600,则椭圆C的离心率为( )| A. | $\frac{\sqrt{3}}{6}$ | B. | $\sqrt{3}$-1 | C. | $\frac{\sqrt{3}}{2}$ | D. | 2-$\sqrt{3}$ |
分析 根据题意,作出椭圆的图形,分析可得△PF1F2为直角三角形,且∠PF1F2=60°,则有|PF1|=c,|PF2|=$\sqrt{3}$c,由椭圆的性质计算可得2a与c的关系,由椭圆的离心率的公式计算可得答案.
解答 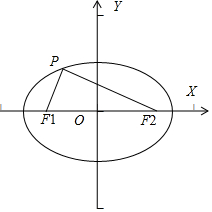 解:根据题意,如图,F1,F2为椭圆C的两个焦点,
解:根据题意,如图,F1,F2为椭圆C的两个焦点,
则|F1F2|=2c,
又由PF1⊥PF2,∠PF1F2=60°,
则△PF1F2为直角三角形,且∠PF1F2=60°,
则有|PF1|=c,|PF2|=$\sqrt{3}$c,
则有2a=|PF1|+|PF2|=($\sqrt{3}$+1)c,
即a=$\frac{\sqrt{3}+1}{2}$c,
则椭圆的离心率e=$\frac{c}{a}$=$\frac{2}{\sqrt{3}+1}$=$\sqrt{3}$-1;
故选:B.
点评 本题考查椭圆的几何性质,注意借助直角三角形的性质分析a、c的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.在等比数列{an}中,“a4,a12是方程x2+3x+1=0的两根”是“a8=±1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
9.在锐角△ABC中,角A,B所对的边分别为a,b,若$2b•sinA=\sqrt{2}a$,则角B等于( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{12}$ |
7.观察下列各等式:$\frac{5}{5-4}$+$\frac{3}{3-4}$=2,$\frac{2}{2-4}$+$\frac{6}{6-4}$=2,$\frac{7}{7-4}$+$\frac{1}{1-4}$=2,$\frac{10}{10-4}$+$\frac{-2}{-2-4}$=2,依照以上各式成立的规律,得到一般性的等式为( )
| A. | $\frac{n}{n-4}$+$\frac{8-n}{8-n-4}$=2 | B. | $\frac{n+1}{n+1-4}$+$\frac{n+1+5}{n+1-4}$=2 | ||
| C. | $\frac{n}{n-4}$+$\frac{n}{n+4-4}$=2 | D. | $\frac{n+1}{n+1-4}$+$\frac{n+5}{n+5-4}$=2 |
8.执行如图所示的程序框图,则输出的S值为( )


| A. | 1009 | B. | -1009 | C. | -1007 | D. | 1008 |