Question

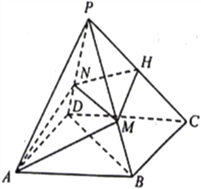
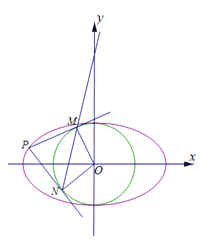
【题目】如图所示，已知A、B、C是长轴长为4的椭圆E上的三点，点A是长轴的一个端点，BC过椭圆中心O，且，|BC|＝2|AC|．

（1）求椭圆E的方程；

（2）在椭圆E上是否存点Q，使得？若存在，有几个（不必求出Q点的坐标），若不存在，请说明理由．

（3）过椭圆E上异于其顶点的任一点P，作的两条切线，切点分别为M、N，若直线MN在x轴、y轴上的截距分别为m、n，证明：为定值．

Answer 1

【答案】（1）（2）满足条件的点Q存在，且有两个（3）见解析，

【解析】试题分析：（1）依题意有，再根据几何条件得三角形AOC为等腰直角三角形，即得点C的坐标，代入椭圆方程可得，（2）先用坐标化简，得点Q在直线上，再根据直线与椭圆位置关系确定交点个数，即得满足条件的点Q个数，（3）设点，先利用两圆公共弦求切点弦MN方程，解得截距，根据点P在椭圆上化简，得定值.

试题解析：(1)依题意知：椭圆的长半轴长，则A(2，0)，

设椭圆E的方程为

由椭圆的对称性知|OC|＝|OB| 又∵，|BC|＝2|AC|

∴AC⊥BC，|OC|＝|AC| ∴△AOC为等腰直角三角形，

∴点C的坐标为(1，1)，点B的坐标为(－1，－1) ，

将C的坐标(1，1)代入椭圆方程得

∴所求的椭圆E的方程为

（2）设在椭圆E上存在点Q，使得，设，则

即点Q在直线上，

∴点Q即直线与椭圆E的交点，

∵直线过点，而点椭圆在椭圆E的内部，

∴满足条件的点Q存在，且有两个．

（3）设点，由M、N是的切点知，,

∴O、M、P、N四点在同一圆上，

且圆的直径为OP,则圆心为，

其方程为，

即-----④

即点M、N满足方程④，又点M、N都在上，

∴M、N坐标也满足方程---------------⑤

⑤-④得直线MN的方程为，

令得，令得，

∴，又点P在椭圆E上，

∴，即=定值.