题目内容
已知
是平面内两个不共线的向量，
=
，
=
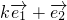，若∥，则实数k的值域是________．
-2
分析：利用向量共线的充要条件列出方程，利用平面向量的基本定理求出k．
解答：
共线则存在λ使
即 =
∴
∴k=-2．
故答案为：-2．
点评：本题考查向量共线的充要条件、平面向量的基本定理，掌握平面内任一向量都可以用两个不平行向量来表示；掌握基底的概念，并能够用基表示平面内的向量．
分析：利用向量共线的充要条件列出方程，利用平面向量的基本定理求出k．
解答：
共线则存在λ使即 =∴
∴k=-2．
故答案为：-2．
点评：本题考查向量共线的充要条件、平面向量的基本定理，掌握平面内任一向量都可以用两个不平行向量来表示；掌握基底的概念，并能够用基表示平面内的向量．
练习册系列答案
相关题目
已知
、
是平面内两个不共线的向量，
=
+5
，
=2
-8
，
=
-
，则（ ）
| a |
| b |
| AB |
| a |
| b |
| BC |
| a |
| b |
| CD |
| a |
| b |
| A、A，B，D三点共线 |
| B、A，C，D三点共线 |
| C、B，C，D三点共线 |
| D、A，B，C三点共线 |
是平面内两个不共线的非零向量，
，
，
，且
三点共线.
的值；
，
，求
的坐标；
，在（2）的条件下，若
四点按逆时针顺序构成平行四边形，
求点A的坐标.
是平面内两个不共线的向量，
=
，
=
，若
∥
，则实数k的值是 ．