Question

【题目】底面是正多边形，顶点在底面的射影是底面中心的棱锥叫正棱锥．已知同底的两个正三棱锥内接于同一个球．已知两个正三棱锥的底面边长为a，球的半径为R．设两个正三棱锥的侧面与底面所成的角分别为α、β，则tan（α+β）的值是 ．

Answer 1

【答案】
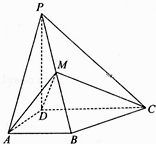
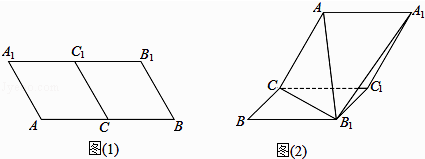
【解析】解：由题意画出图象如下图：

由图得，右侧为该球过SA和球心的截面，由于三角形ABC为正三角形，
所以D为BC中点，且AD⊥BC，SD⊥BC，MD⊥BC，
故∠SDA=α，∠MDA=β．
设SM∩平面ABC=P，则点P为三角形ABC的重心，且点P在AD上，SM=2R，AB=a，
∴ ，
因此
= ，
所以答案是： ．
【考点精析】根据题目的已知条件，利用两角和与差的正切公式和球内接多面体的相关知识可以得到问题的答案，需要掌握两角和与差的正切公式：；球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长．